【昇腾CANN训练营·第十二期】告别无从下手：拆解开源Cube算子，快速掌握开发要领

摘要：2025年昇腾CANN训练营推出Cube算子开发专题课程，重点讲解基于Matmul高阶API的矩阵乘法开发。相比Vector算子，Cube算子开发面临数据流复杂、格式转换和三维Tiling等挑战。文章通过实例解析Matmul API的使用方法，包括类定义、Tiling参数配置和自动执行流程，将Cube开发简化为"定义类-配参数-一键跑"三个步骤。训练营提供AscendC算

一行袋码

140人浏览 · 2025-11-28 16:16:29

一行袋码 · 2025-11-28 16:16:29 发布

训练营简介 2025年昇腾CANN训练营第二季，基于CANN开源开放全场景，推出0基础入门系列、码力全开特辑、开发者案例等专题课程，助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证，即可领取精美证书，完成社区任务更有机会赢取华为手机，平板、开发板等大奖。

报名链接：https://www.hiascend.com/developer/activities/cann20252#cann-camp-2502-intro

前言

在深度学习中，90% 以上的计算量都来自于矩阵乘法（Matrix Multiplication）。昇腾 AI Core 专门为此设计了强大的 Cube 单元。

对于 Ascend C 开发者来说，开发 Cube 算子的难度远高于 Vector 算子：

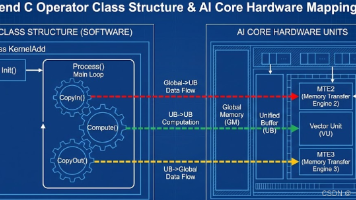
数据流更长：数据不再是简单的 GM <-> UB，而是涉及 GM -> L1 -> L0A/L0B -> L0C -> GM 的复杂搬运。
数据格式特殊：为了适配 Cube 单元的硬件物理排布，数据通常需要转换为 Fractal（分形）格式（如 zZ, nZ），而非人类直观理解的 ND 格式。
Tiling 维度增加：不再是切一刀，而是要在 M、N、K 三个轴上进行切分。

幸运的是，Ascend C 提供了基于模板的 Matmul 高阶 API。它帮我们封装了 99% 的底层细节（包括内存管理、格式转换、流水线同步），让我们像写 Python 一样轻松调用矩阵乘法。

本期文章，我们将“解剖”一个标准的 Matmul 算子样例，带你快速上手。

一、核心概念：Matmul API 的“黑盒”模型

在 Vector 编程中，我们需要手动管理 CopyIn, Compute, CopyOut。而在 Cube 编程中，Ascend C 提供了一个核心类：Matmul。

你可以把它想象成一个全自动的面包机：

原料：Tensor A（左矩阵 $M \times K$），Tensor B（右矩阵 $K \times N$）。
设置：Tiling 参数（怎么切面包）。
输出：Tensor C（结果矩阵 $M \times N$）。

我们只需要把数据塞给这个对象，调用 Iterate（迭代），它就会自动在 AI Core 内部完成所有流水线操作。

二、庖丁解牛：拆解标准 Matmul 算子

我们以一个基础的 $C = A \times B + Bias$ 为例，看看代码结构是怎样的。

2.1 算子类定义：引入 Matmul 模板

头文件引入是第一步，Cube 开发需要包含 lib/matmul_intf.h。

#include "kernel_operator.h"
#include "lib/matmul_intf.h" // 关键头文件

using namespace AscendC;

// 定义 Matmul 实例的类型
// 参数模版：<位置, 格式, 数据类型>
// aType/bType/cType/biasType: 指定各操作数的数据类型
typedef MatmulType<AscendC::TPosition::GM, CubeFormat::ND, half> aType;
typedef MatmulType<AscendC::TPosition::GM, CubeFormat::ND, half> bType;
typedef MatmulType<AscendC::TPosition::GM, CubeFormat::ND, float> cType; // 累加器通常用 FP32
typedef MatmulType<AscendC::TPosition::GM, CubeFormat::ND, half> biasType;

class MatmulKernel {
public:
    // ... Init 和 Process ...
private:
    // 声明 Matmul 对象实例
    // 第一个模板参数必须是 MatmulType 的组合
    Matmul<aType, bType, cType, biasType> mm;
    
    // 全局内存指针
    GlobalTensor<half> aGlobal;
    GlobalTensor<half> bGlobal;
    GlobalTensor<float> cGlobal; 
    // ...
};

解析：这里最关键的是 Matmul<...> 对象的声明。通过模板参数，我们告诉编译器输入在 GM 上，格式是 ND（API 会自动处理到私有格式的转换），这极大地简化了开发。

2.2 Init 函数：配置 Tiling 与绑定 Tensor

Cube 算子的 Tiling 参数比 Vector 复杂，包含 stepM, stepN, stepK 等，用于指导矩阵的分块。

__aicore__ inline void Init(GM_ADDR a, GM_ADDR b, GM_ADDR c, GM_ADDR bias, TilingData tiling) {
    // 1. 初始化 Global Tensor
    aGlobal.SetGlobalBuffer((__gm__ half*)a);
    bGlobal.SetGlobalBuffer((__gm__ half*)b);
    cGlobal.SetGlobalBuffer((__gm__ float*)c);
    
    // 2. 配置 Matmul 对象的 Tiling 参数
    // 这些参数通常由 Host 侧计算并下发
    mm.SetSubBlockIdx(0); // 单核场景设为0
    
    // 设置矩阵维度 M, N, K
    mm.SetIntrinShape(tiling.M, tiling.N, tiling.K);
    
    // 设置分块策略 (关键！)
    // StepM/N/K 决定了单次迭代处理的 Base Block 大小
    mm.SetTemplateShape(tiling.stepM, tiling.stepN, tiling.stepK);
    
    // 3. 绑定 Global Tensor 到 Matmul 对象
    // 告诉对象数据在哪里
    mm.SetTensorA(aGlobal);
    mm.SetTensorB(bGlobal);
    // mm.SetBias(biasGlobal); // 如果有 Bias
}

2.3 Process 函数：一键执行

到了 Process 阶段，代码反而比 Vector 算子更简单。你不需要手写 CopyIn -> Compute -> CopyOut 的流水线，Matmul 对象内部已经封装好了。

__aicore__ inline void Process() {
    // 1. 自动迭代计算
    // IterateAll 会根据 Tiling 参数，自动循环处理所有分块
    // 内部自动处理 GM -> L1 -> L0 的搬运和计算
    mm.IterateAll(cGlobal);
    
    // 或者，如果你需要更细粒度的控制（例如计算后加个 Relu 再输出），可以使用分步接口：
    /*
    while (mm.Iterate()) {
        mm.GetResult(cLocal); // 获取局部结果到 UB
        Relu(cLocal, cLocal, ...); // 在 UB 上做 Vector 运算
        DataCopy(cGlobal, cLocal, ...); // 手动搬运回 GM
    }
    */
}