数字是宇宙的音符，而数论则是这些音符背后的严密乐谱。

---

前言

在鸿蒙（OpenHarmony）应用开发中，我们无时无刻不在与“唯一性”打交道：如何为每一个 Widget 分配唯一的 Key？如何确保本地缓存的文件没有被篡改？如何在高并发的数据库查询中快速定位记录？

这些问题的核心指向了离散数学中一个古老而深邃的分支——数论（Number Theory）。通过同余理论、素数分布以及哈希函数的数学构造，我们可以构建出高效且防碰撞的唯一性标识系统。本篇将带你揭开数字背后的哈希真相。

---

目录

1. 同余理论：哈希函数的数学根基
2. 素数的魅力：为何哈希表大小偏爱素数
3. 系统架构设计 (UML & 流程)
4. Flutter 核心代码实现：自定义 Key 生成逻辑
5. 实战案例演练：文件完整性与哈希碰撞模拟
6. 总结与展望

---

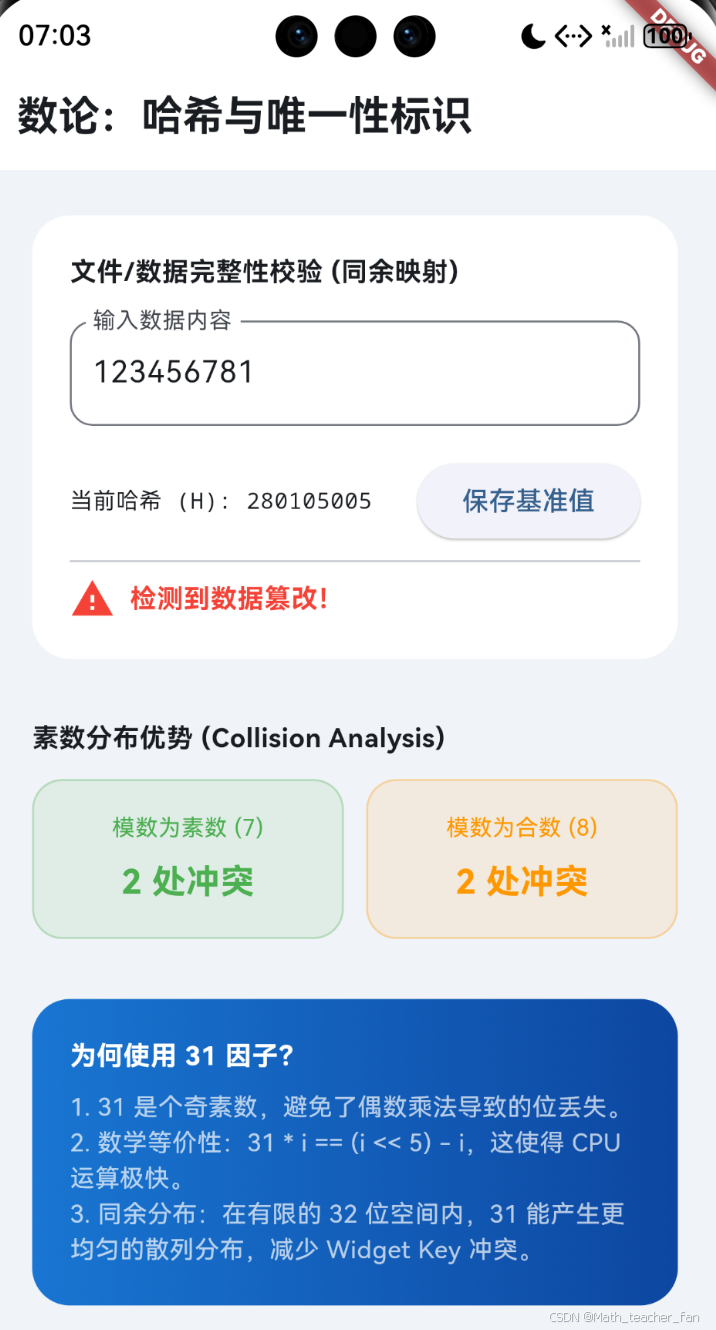
点击保存基准值，再进行修改。

一、 同余理论：哈希函数的数学根基

在数论中，给定一个正整数 $m$，如果两个整数 $a$ 和 $b$ 满足 $a-b$ 能被 $m$ 整除，即：
[ a \equiv b \pmod m ]
我们称 $a$ 与 $b$ 对模 $m$ 同余。

1. 哈希映射与同余

哈希函数的本质是一个从大空间到小空间的映射 $h(k)=k(\mathrm{mod}m)$。

• 冲突 (Collision)：当 $k_1\equiv k_2(\mathrm{mod}m)$ 时，发生哈希碰撞。
• 业务映射：在 Flutter 的 Map 存储或 Widget 局部刷新中，哈希算法决定了数据的存取效率。

---

二、 素数的魅力：为何哈希表大小偏爱素数

为什么许多底层算法（如 Java 的 HashMap 旧版或某些缓存算法）在设置哈希表大小时倾向于使用素数 (Prime Number)？

1. 均匀分布原理

若哈希表大小 $m$ 是一个素数，且哈希函数采用 $h(k)=k(\mathrm{mod}m)$，则对于具有某种规律的输入序列（如 { 10 , 20 , 30 , …   } \{10, 20, 30, \dots\} {10,20,30,…}），只要步长与 $m$ 互质，冲突的概率就会大大降低。

2. Widget Key 的散列

在 Flutter 中，ValueKey 或 ObjectKey 的 hashCode 运算往往涉及素数的乘法（如著名的 31 因子：h = 31 * h + c），这是为了利用素数在二进制位移中的散列特性，使 Key 在哈希空间中分布更均匀。

---

三、 系统架构设计

我们要构建一个模拟哈希桶与 Key 生成的分析器。

1. 业务流程图 (Flowchart)

2. 系统类图 (UML)

---

四、 Flutter 核心代码实现：自定义 Key 生成逻辑

模拟一个基于数论原理的简单散列 Key 生成。

核心代码片段：

// 1. 模拟 31-Hash 算法 (经典的数论应用)
int generateHashCode(String input) {
  int h = 0;
  for (int i = 0; i < input.length; i++) {
    // 31 是一个奇素数，31 * i = (i << 5) - i，编译器优化极佳
    h = 31 * h + input.codeUnitAt(i);
  }
  return h;
}

// 2. 文件完整性校验 (同余思想的延伸)
bool verifyData(String data, int expectedHash) {
  return generateHashCode(data) == expectedHash;
}

---

五、 实战案例演练

在 lib/main.dart 中，我们实现了一个名为 “Harmony Hash Lab” 的系统：

1. 哈希碰撞可视化：模拟不同大小（素数 vs 合数）的哈希表在处理同一批数据时的冲突率。
2. Widget Key 动态演示：展示在动态列表中，唯一的哈希 Key 如何保证状态不丢失。
3. 同余校验器：输入一段文本，实时计算其哈希值并进行模拟的“文件完整性”验证。

---

六、 总结与展望

数论是构建稳定标识系统的数学地基。

• 效率：利用素数和位运算，实现纳秒级的唯一性判定。
• 安全：同余理论和不可逆哈希是数据完整性校验的核心。
• 秩序：在混乱的数据海洋中，数论为每一个对象指明了其唯一的物理归宿。

下一篇预告：我们将迎来本专栏的收官之作——计算复杂度 (Big O)，看数学如何量化鸿蒙系统在低功耗模式下的渲染性能极限。

---

欢迎加入开源鸿蒙跨平台社区：https://openharmonycrossplatform.csdn.net