万物皆有联系，而联系的本质是关系。理解等价类，就是理解数据的归宿。

---

前言

在鸿蒙（OpenHarmony）分布式系统的开发中，我们经常面临一个棘手的问题：数据一致性。同一份数据可能散落在手机、平板、手表等多个节点上。当我们说“这两个对象是同一个实体”时，我们实际上在探讨离散数学中的二元关系（Binary Relation）。

特别是**等价关系（Equivalence Relation）与商集（Quotient Set）**的概念，它们为处理跨端冲突、本地数据库关联查询以及大规模数据去重提供了严密的数学模型。本篇将带你通过“关系”的视角，重构你的数据层代码。

---

目录

1. 二元关系的基础性质
2. 等价关系与商集：分类的数学本质
3. 系统架构设计 (UML & 流程)
4. Flutter 核心代码实现：等价类合并算法
5. 实战案例演练：分布式数据冲突处理
6. 总结与展望

---

一、 二元关系的基础性质

设 $A$ 是一个集合，$A$ 上的二元关系 $R$ 是笛卡尔积 $A\times A$ 的子集。如果一个关系满足以下三个性质，我们称之为等价关系：

1. 自反性 (Reflexivity)：对于每个 $a\in A$，有 $(a,a)\in R$。
   • 业务对应：任何数据对象都与其自身相等。
2. 对称性 (Symmetry)：若 $(a,b)\in R$，则必有 $(b,a)\in R$。
   • 业务对应：如果 A 是 B 的镜像，则 B 也是 A 的镜像。
3. 传递性 (Transitivity)：若 $(a,b)\in R$ 且 $(b,c)\in R$，则必有 $(a,c)\in R$。
   • 业务对应：跨端同步的传递性——如果手机同步给平板，平板同步给手表，则手机数据与手表数据等价。

---

二、 等价关系与商集：分类的数学本质

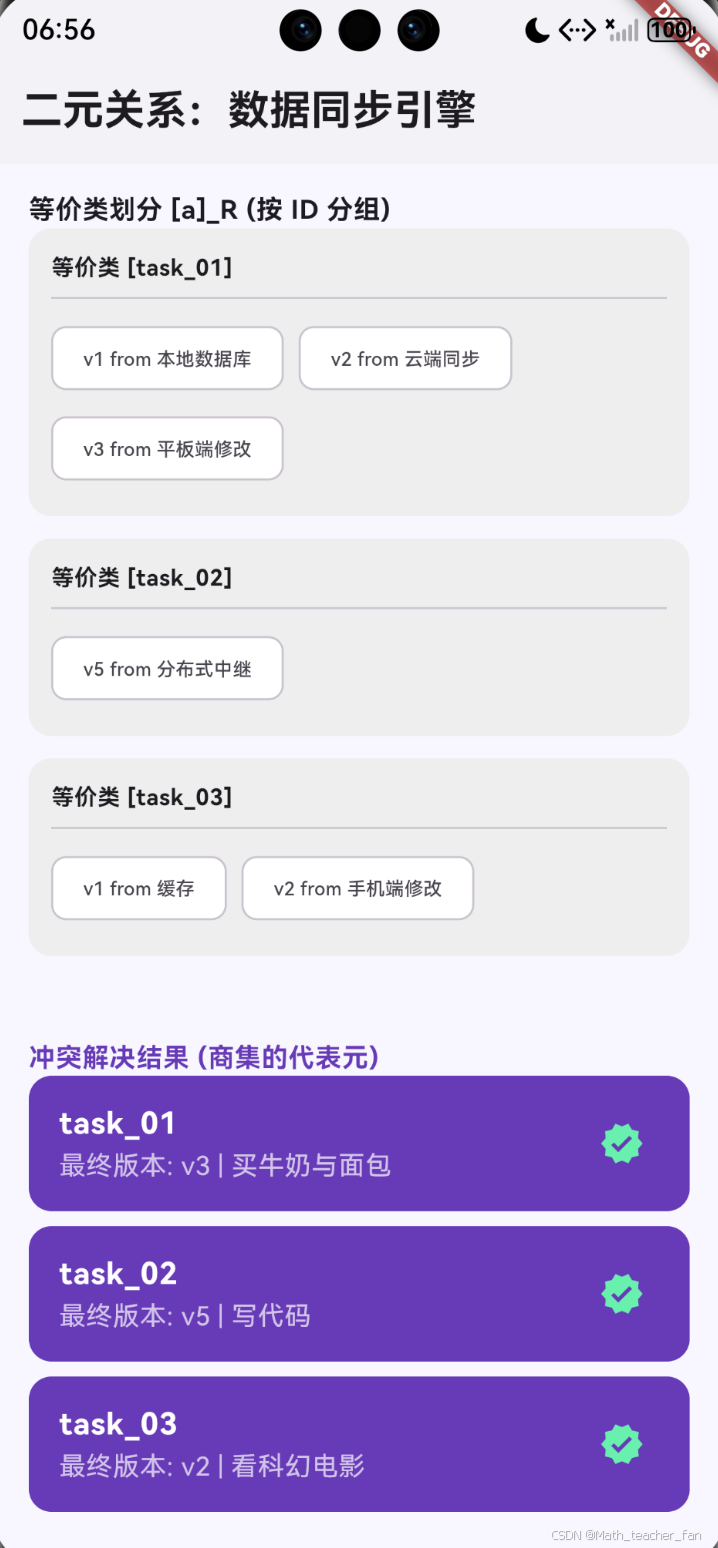
一个等价关系 $R$ 会将集合 $A$ 划分为若干个不相交的子集，每个子集称为一个等价类 (Equivalence Class)，记作 $[a{]}_R$。所有这些等价类的集合称为 $A$ 关于 $R$ 的商集 (Quotient Set)，记作 $A/R$。

在 Flutter 中的应用：

• 数据去重：将所有 ID 相同的不同版本对象视为一个等价类，从每个类中提取最新的版本，即完成了商集的构建。
• 关联分组：按分类（Category）建立关系，商集就是我们 UI 列表中的“分组（Group）”。

---

三、 系统架构设计

我们要构建一个处理分布式冲突的数据引擎，基于“实体 ID”建立等价关系。

1. 业务流程图 (Flowchart)

2. 系统类图 (UML)

---

四、 Flutter 核心代码实现：等价类合并算法

利用 groupBy 思想构建商集，实现冲突解决。

核心代码片段：

// 1. 定义等价关系：实体 ID 相同即视为属于同一等价类
bool isEquivalent(Entity a, Entity b) => a.id == b.id;

// 2. 构建商集并合并 (模拟冲突处理)
List<Entity> resolve(List<Entity> allData) {
  Map<String, List<Entity>> quotientSet = {};
  
  // 划分为等价类 (Grouping by ID)
  for (var entity in allData) {
    (quotientSet[entity.id] ??= []).add(entity);
  }

  // 从每个等价类中选取最优解 (例如：版本最高者)
  return quotientSet.values.map((group) {
    return group.reduce((a, b) => a.version > b.version ? a : b);
  }).toList();
}

---

五、 实战案例演练

在 lib/main.dart 中，我们实现了一个名为 “Harmony Data Resolver” 的系统：

1. 多源数据模拟：从“本地数据库”、“云端缓存”、“鸿蒙分布式中继”三个来源获取同一批数据。
2. 等价关系判定：即使对象内存地址不同，只要业务 ID 相同，就划入同一个等价类。
3. 商集可视化：界面清晰展示每个等价类的成员，并演示如何基于商集自动选出“真值”进行最终渲染。

---

六、 总结与展望

二元关系是描述数据世界关联性的数学底层。

• 稳定性：通过等价关系的传递性，保证了分布式环境下数据的一致性边界。
• 结构化：通过商集的概念，将凌乱的数据流自动组织成有序的分组。
• 严密性：用数学思维代替拍脑袋的逻辑，让冲突处理变得可证明。

下一篇预告：我们将步入数论基础（Number Theory），看哈希算法、素数与同余理论如何支撑起鸿蒙系统的唯一性标识与缓存策略。

---

欢迎加入开源鸿蒙跨平台社区：https://openharmonycrossplatform.csdn.net