有限的元素，无限的排布。排列组合是生成多样化 UI 的数学引擎。

---

前言

在追求极致体验的鸿蒙（OpenHarmony）应用开发中，“灵动”与“多样性”是高级感的核心。为什么有些瀑布流布局百看不厌？为什么有些动态主题色调总是和谐？这背后的功臣是离散数学中的组合数学（Combinatorics）。

通过排列（Permutations）与组合（Combinations），我们可以通过极少的基础素材（如 5 种基础色、3 种卡片尺寸），推导出成千上万种不重复的视觉呈现方案。本篇将深入探讨排列组合原理，并演示如何将其应用于动态皮肤生成与瀑布流布局。

---

目录

1. 排列与组合的数学定义
2. 二项式定理与 UI 概率空间
3. 系统架构设计 (UML & 流程)
4. Flutter 核心代码实现：组合生成算法
5. 实战案例演练：动态主题色与随机瀑布流
6. 总结与展望

---

一、 排列与组合的数学定义

1. 排列 (Permutation, $P$)

从 $n$ 个不同元素中取出 $m$ 个元素，并按特定顺序排成一列。

业务场景：多图轮播的顺序、用户自定义底部导航栏的图标排序。

2. 组合 (Combination, $C$)

从 $n$ 个不同元素中取出 $m$ 个元素，不考虑顺序。

业务场景：从 10 种颜色中随机挑选 3 种作为主题色、在 50 种商品中抽选 5 种做限时抢购。

---

二、 二项式定理与 UI 概率空间

二项式定理描述了 $(x+y{)}^n$ 的展开。在 UI 开发中，它常用于计算复合状态的分布。
例如，如果一个组件有 4 个可独立切换的开关（如：圆角/直角、有阴影/无阴影等），其总组合数即为 $2^n$（基于二项式系数的和 $\sum \left(\genfrac{}{}{0ex}{}{n}{k}\right)=2^n$）。理解这种分布有助于我们设计更具鲁棒性的单元测试用例。

---

三、 系统架构设计

我们要构建一个动态布局生成器。

1. 业务流程图 (Flowchart)

2. 系统类图 (UML)

---

四、 Flutter 核心代码实现：组合生成算法

在 Flutter 中，我们可以编写通用的组合生成器来驱动 UI。

核心代码片段：

// 1. 随机打乱序列 (全排列的一个随机实例)
List<T> shuffle<T>(List<T> items) {
  var list = List<T>.from(items);
  list.shuffle(); // 基于 Fisher-Yates 算法
  return list;
}

// 2. 从集合中随机取 k 个元素 (组合的一个实例)
List<T> sample<T>(List<T> items, int k) {
  if (k > items.length) return items;
  var list = List<T>.from(items);
  list.shuffle();
  return list.take(k).toList();
}

---

五、 实战案例演练

在 lib/main.dart 中，我们实现了一个名为 “Harmony Layout Explorer” 的系统：

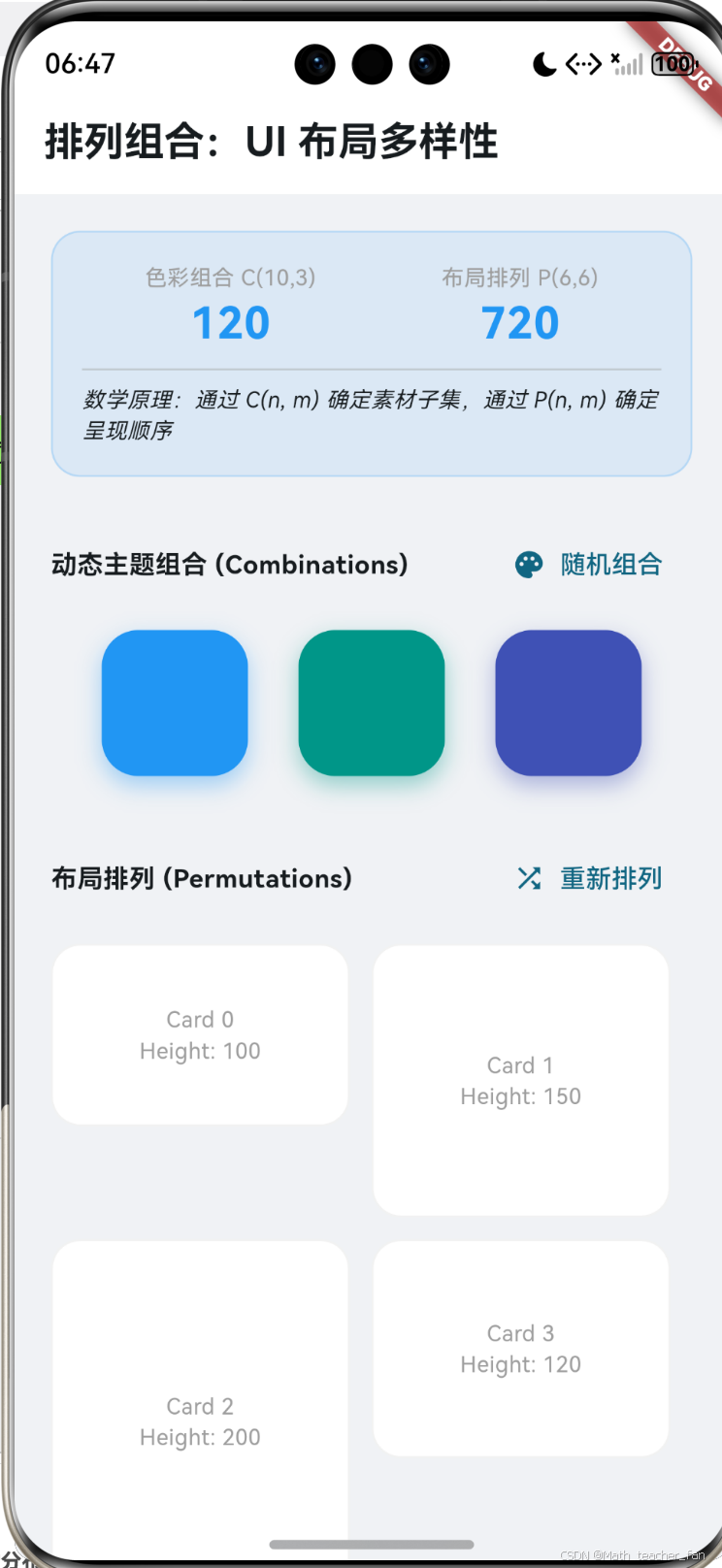
1. 动态色彩组合：从一个精心挑选的调色板（$n=10$）中，基于 $C(10,3)$ 随机生成 120 种可能的皮肤配色方案。
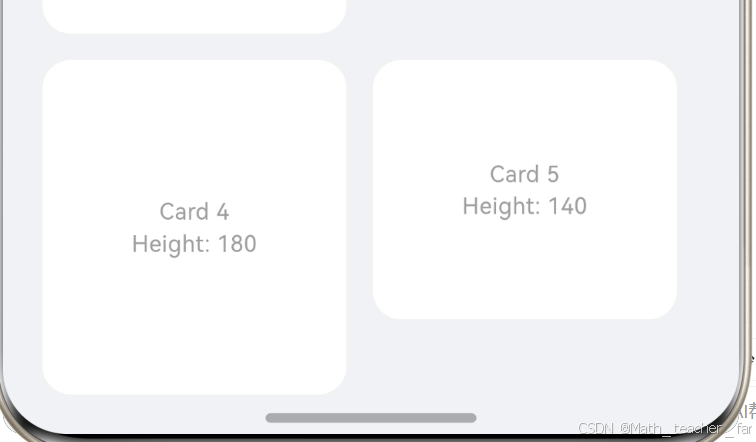
2. 随机高度瀑布流：模拟瀑布流卡片的排列。通过对宽度和高度的随机排列，展示如何利用组合数学打破视觉疲劳。
3. 排列组合计算器：实时计算 $P(n,m)$ 和 $C(n,m)$，让开发者直观感受到 UI 可能性的指数级增长。

---

六、 总结与展望

排列组合是解决“素材少、需求多”的核心良药。

• 视觉多样性：通过简单的数学变换，实现“千人千面”的个性化布局。
• 测试覆盖率：通过计算组合总数，帮助开发者设计更完备的边缘测试。
• 动态性能：理解排列逻辑有助于优化列表的 Diff 算法。

下一篇预告：我们将回归数学的底层关系——二元关系与等价类，探讨如何在鸿蒙分布式设备间进行高效的数据同步与冲突处理。

---

欢迎加入开源鸿蒙跨平台社区：https://openharmonycrossplatform.csdn.net