如果说集合论定义了数据的边界，那么命题逻辑则主导了 UI 状态的流转。

---

前言

在 Flutter 鸿蒙开发中，我们经常遇到这样的场景：一个按钮的启用状态取决于多个条件的组合——“用户已登录” AND (“手机号已验证” OR “三方授权完成”) AND NOT “被封禁”。随着业务复杂度的增加，传统的 if-else 嵌套会迅速演变成难以维护的“代码地狱”。

命题逻辑（Propositional Logic） 及其核心 布尔代数（Boolean Algebra） 为我们提供了重构这些复杂判断的数学武器。通过德·摩根定律（De Morgan’s laws）等真值变换，我们可以将冗长的逻辑链条简化为优雅的表达式，从而构建出更加健壮、高性能的响应式引擎。

---

目录

1. 命题逻辑的基础算子
2. 布尔代数与德·摩根定律的应用
3. 系统架构设计 (UML & 流程)
4. Flutter 核心代码实现：逻辑重构实战
5. 实战案例演练：动态表单校验引擎
6. 总结与展望

---

一、 命题逻辑的基础算子

在离散数学中，命题是具有确切真值的陈述句。我们将 UI 中的每个状态判定（如 isLoggedIn）视为一个原子命题。

1. 核心联结词

联结词	符号	Flutter 操作符	描述	业务场景
合取 (Conjunction)	$p\wedge q$	&&	且：两者皆为真	注册：填了手机号 且 勾选协议
析取 (Disjunction)	$p\vee q$	`		`
否定 (Negation)	$\neg p$	!	非：真值取反	错误展示：NOT 正在加载
蕴含 (Implication)	$p\to q$	`!p		q`

---

二、 布尔代数与德·摩根定律的应用

在复杂的响应式布局中，我们经常需要处理“反向逻辑”（例如：什么时候隐藏组件）。这时，德·摩根定律 显得尤为重要：

1. 第一定律：$\neg (p\wedge q)\equiv \neg p\vee \neg q$
   • 语义：不满足（条件 A 且 条件 B），等价于（不满足 A 或 不满足 B）。
2. 第二定律：$\neg (p\vee q)\equiv \neg p\wedge \neg q$
   • 语义：不满足（条件 A 或 条件 B），等价于（既不满足 A 且 也不满足 B）。

实战价值：利用这些定律，我们可以将复杂的 !(a && b) 转换为 !a || !b，使代码更符合人类的阅读直觉。

---

三、 系统架构设计

为了实现一个逻辑严密的响应式校验引擎，我们需要定义清晰的命题流向。

1. 业务流程图 (Flowchart)

2. 系统类图 (UML)

---

四、 Flutter 核心代码实现：逻辑重构实战

我们来看如何将一段“地狱式”代码通过命题逻辑重构。

1. 重构前（嵌套地狱）

if (isLoggedIn) {
  if (hasPermission) {
    if (!isBanned) {
      showDeleteButton = true;
    } else {
      showDeleteButton = false;
    }
  } else {
    showDeleteButton = false;
  }
}

2. 重构后（逻辑蕴含与合取）

// 使用合取逻辑一气呵成
bool get showDeleteButton => isLoggedIn && hasPermission && !isBanned;

// 使用蕴含逻辑重构：若要提交(q)，必须先勾选协议(p)
// 公式：p -> q (即 !p || q)
bool get isSubmitValid => !isAgreed ? false : isFormFilled;

---

五、 实战案例演练

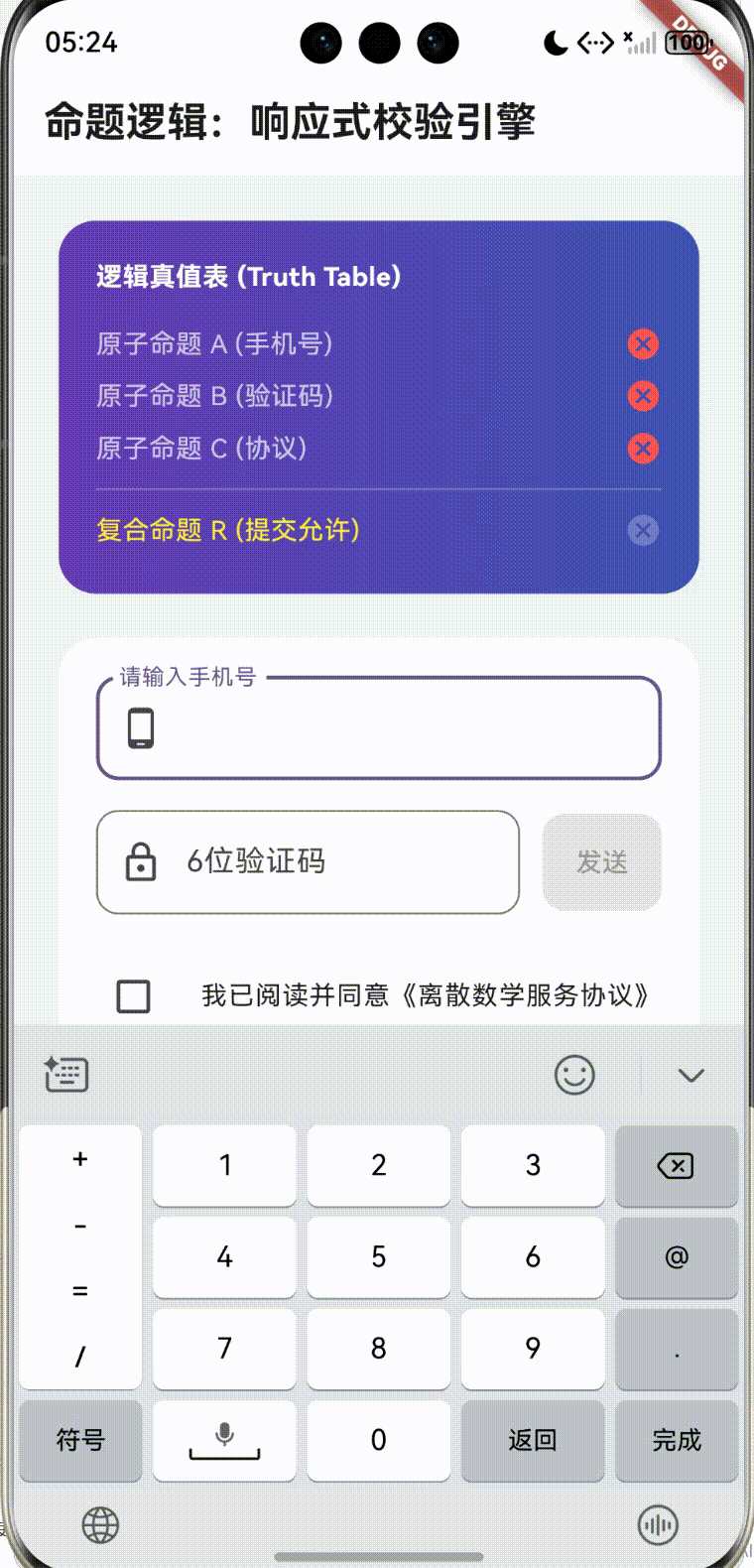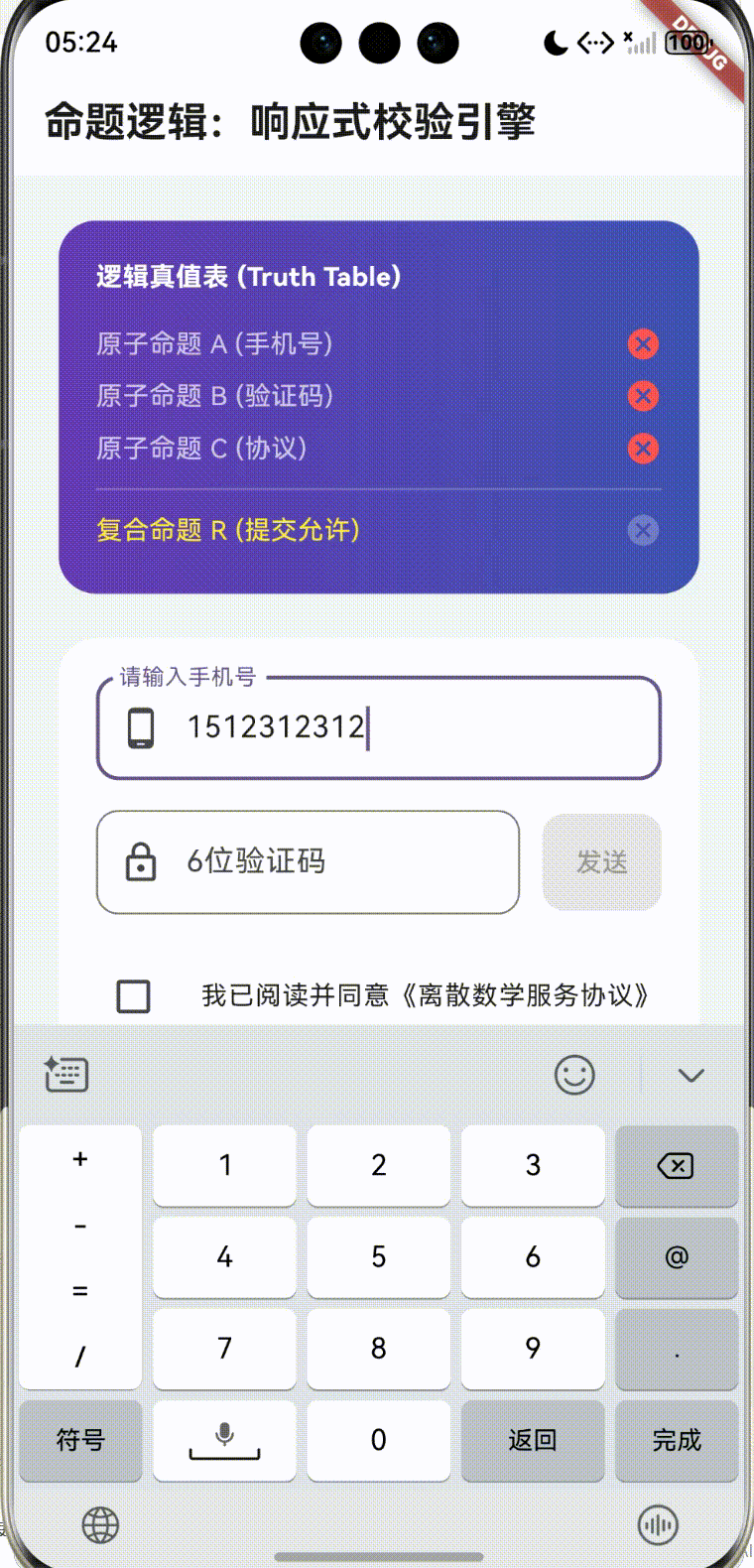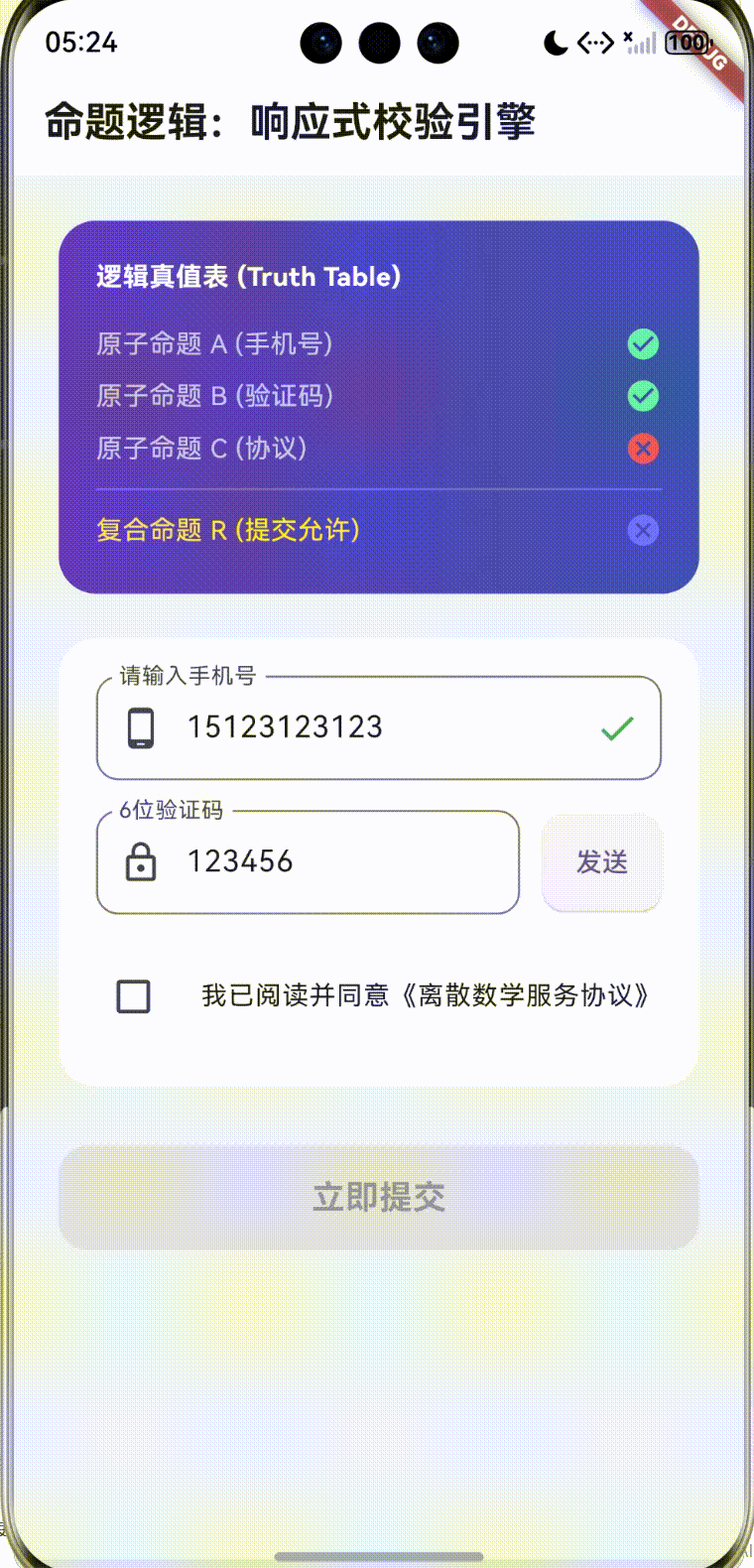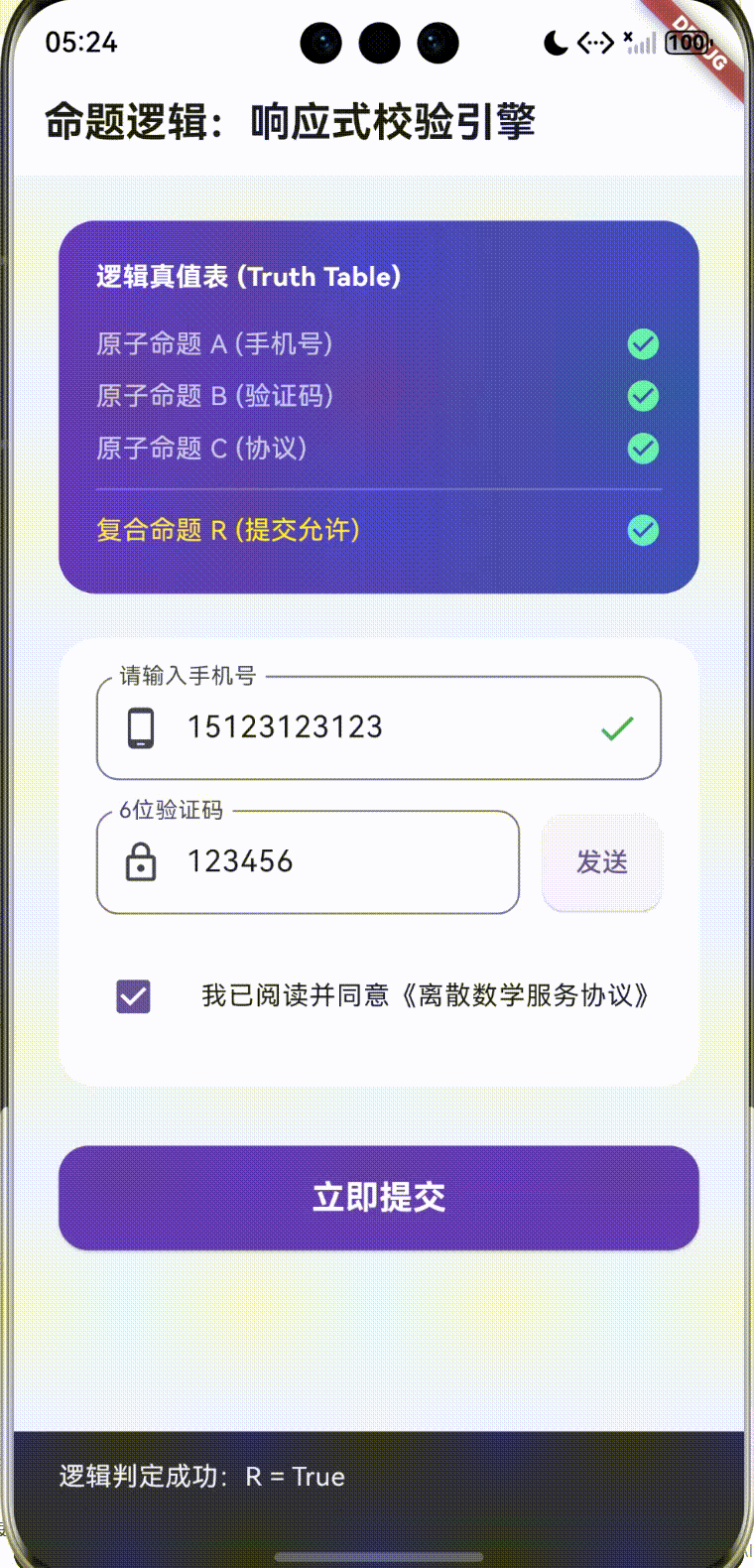
在 lib/main.dart 中，我们实现了一个名为 “Harmony Logic Validator” 的页面。该页面模拟了一个复杂的注册表单：

• 原子命题 A：手机号格式正确。
• 原子命题 B：验证码已填写。
• 原子命题 C：用户已阅读并同意协议。
• 复合命题 R：$R=A\wedge B\wedge C$（只有三者皆真，提交按钮才激活）。

同时，我们展示了逻辑蕴含的应用：如果“手机号”不正确，则直接通过“否定”逻辑屏蔽掉“验证码发送”命题。

---

六、 总结与展望

命题逻辑不仅是数学课本上的公式，更是构建高性能 Flutter 响应式应用的工具。

• 原子性：将 UI 状态拆分为最小命题，便于单独维护。
• 组合性：通过算子灵活组合，应对千变万化的业务需求。
• 健壮性：利用数学等价式（如德·摩根定律）简化逻辑，减少 Bug 发生率。

下一篇预告：我们将跨入**图论（Graph Theory）**的世界，看它如何主导 Flutter 的路由导航与插件依赖树。

---

欢迎加入开源鸿蒙跨平台社区：https://openharmonycrossplatform.csdn.net