第一章 矩阵乘法在AI计算中的核心地位

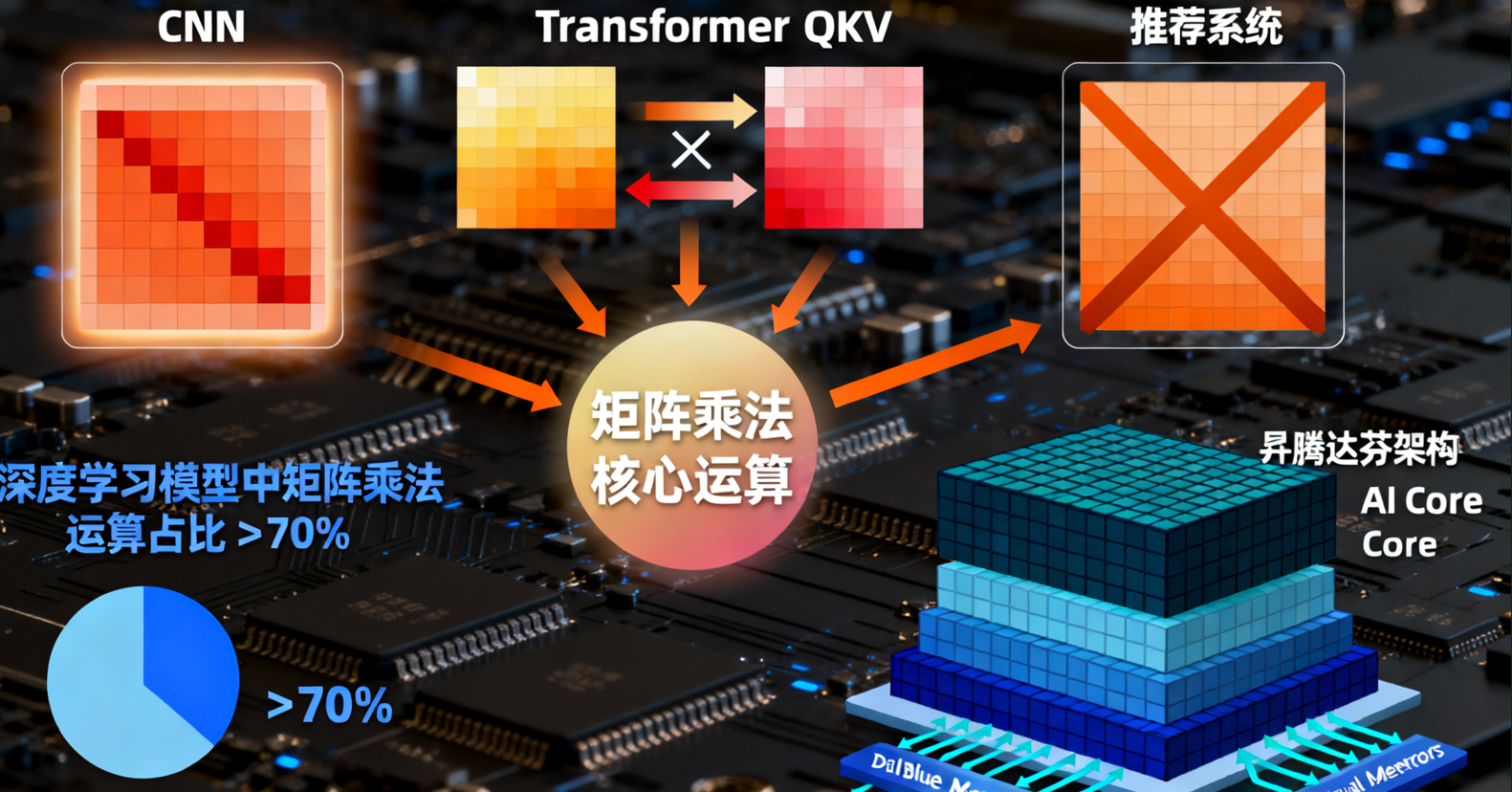
        矩阵乘法是人工智能计算中最基础、最核心的运算操作之一。从卷积神经网络中的卷积运算，到Transformer模型中的自注意力机制，再到推荐系统中的特征交叉计算，矩阵乘法都扮演着不可或缺的角色。在现代深度学习模型中，矩阵乘法运算通常占据了超过70%的计算量，其性能直接影响着整个模型的推理效率和训练速度。

        矩阵乘法的数学基础可以表示为：对于两个矩阵A（M×K）和B（K×N），它们的乘积C（M×N）中的每个元素计算为C[i][j] = Σ(A[i][k] * B[k][j])，其中k从0到K-1。这个看似简单的运算却蕴含着巨大的计算复杂度和优化空间。

        矩阵乘法的计算特性使其成为衡量AI加速器性能的重要基准。首先，它具有O(MNK)的计算复杂度，但只有O(MK + KN + M*N)的内存访问量，这为计算优化提供了理论上的优势。其次，矩阵乘法具有规则的数据访问模式，适合进行向量化和并行化优化。再者，通过分块技术可以充分利用缓存局部性，大幅提升计算效率。

        在昇腾AI处理器上开发高性能的矩阵乘自定义算子，需要深入理解硬件架构特性。达芬奇架构采用计算立方体设计，专门针对矩阵运算进行了优化。每个AI Core包含强大的矩阵计算单元，支持高效的并行处理。同时，层次化的存储体系（全局内存、本地内存、寄存器）为数据重用提供了有力支持。

第二章 Ascend C矩阵乘算子基础实现

2.1 基础矩阵乘法实现

让我们从最简单的矩阵乘法实现开始，理解Ascend C编程的基本模式：

#include <aicore/vector_operations.h>
#include <aicore/memory_operations.h>

extern "C" __global__ __aicore__ void naive_matmul_kernel(
    uint32_t blockDim, 
    uint32_t l2ctrl, 
    uint32_t buffer, 
    uint32_t length,
    int32_t M, int32_t N, int32_t K) {
    
    // 获取任务ID
    uint32_t task_id = get_task_id();
    uint32_t task_num = get_task_num();
    
    // 计算每个任务处理的行数
    int32_t rows_per_task = (M + task_num - 1) / task_num;
    int32_t start_row = task_id * rows_per_task;
    int32_t end_row = min(start_row + rows_per_task, M);
    
    // 获取全局内存地址
    GM_ADDR A_gm = GET_GLOBAL_BUFFER(buffer);
    GM_ADDR B_gm = A_gm + M * K * sizeof(float);
    GM_ADDR C_gm = B_gm + K * N * sizeof(float);
    
    // 本地内存用于数据块
    __local__ float A_tile[16][16];
    __local__ float B_tile[16][16];
    __local__ float C_tile[16][16];
    
    // 处理分配的行
    for (int i = start_row; i < end_row; i += 16) {
        for (int j = 0; j < N; j += 16) {
            // 初始化累加器
            for (int ti = 0; ti < 16; ++ti) {
                for (int tj = 0; tj < 16; ++tj) {
                    C_tile[ti][tj] = 0.0f;
                }
            }
            
            // 分块矩阵乘法
            for (int k = 0; k < K; k += 16) {
                // 加载A的数据块
                for (int ti = 0; ti < 16; ++ti) {
                    for (int tk = 0; tk < 16; ++tk) {
                        int global_i = i + ti;
                        int global_k = k + tk;
                        if (global_i < M && global_k < K) {
                            A_tile[ti][tk] = ((float*)A_gm)[global_i * K + global_k];
                        } else {
                            A_tile[ti][tk] = 0.0f;
                        }
                    }
                }
                
                // 加载B的数据块
                for (int tk = 0; tk < 16; ++tk) {
                    for (int tj = 0; tj < 16; ++tj) {
                        int global_k = k + tk;
                        int global_j = j + tj;
                        if (global_k < K && global_j < N) {
                            B_tile[tk][tj] = ((float*)B_gm)[global_k * N + global_j];
                        } else {
                            B_tile[tk][tj] = 0.0f;
                        }
                    }
                }
                
                // 计算分块乘积
                for (int ti = 0; ti < 16; ++ti) {
                    for (int tj = 0; tj < 16; ++tj) {
                        for (int tk = 0; tk < 16; ++tk) {
                            C_tile[ti][tj] += A_tile[ti][tk] * B_tile[tk][tj];
                        }
                    }
                }
            }
            
            // 写回结果
            for (int ti = 0; ti < 16; ++ti) {
                for (int tj = 0; tj < 16; ++tj) {
                    int global_i = i + ti;
                    int global_j = j + tj;
                    if (global_i < M && global_j < N) {
                        ((float*)C_gm)[global_i * N + global_j] = C_tile[ti][tj];
                    }
                }
            }
        }
    }
}

这个基础实现虽然功能正确，但性能并不理想。它存在几个关键问题：内存访问模式不佳、计算资源利用率低、缺乏向量化优化等。接下来我们将逐步优化这个实现。

2.2 优化后的矩阵乘法实现

class OptimizedMatMul {
private:
    static constexpr int BLOCK_SIZE = 64;
    static constexpr int VECTOR_SIZE = 8;
    
public:
    __global__ __aicore__ void optimized_matmul_kernel(
        uint32_t blockDim, uint32_t l2ctrl, uint32_t buffer, uint32_t length,
        int32_t M, int32_t N, int32_t K) {
        
        uint32_t task_id = get_task_id();
        uint32_t task_num = get_task_num();
        
        // 更精细的任务划分
        int32_t total_blocks = (M + BLOCK_SIZE - 1) / BLOCK_SIZE * 
                              (N + BLOCK_SIZE - 1) / BLOCK_SIZE;
        int32_t blocks_per_task = (total_blocks + task_num - 1) / task_num;
        int32_t start_block = task_id * blocks_per_task;
        int32_t end_block = min(start_block + blocks_per_task, total_blocks);
        
        GM_ADDR A_gm = GET_GLOBAL_BUFFER(buffer);
        GM_ADDR B_gm = A_gm + M * K * sizeof(float);
        GM_ADDR C_gm = B_gm + K * N * sizeof(float);
        
        // 双缓冲本地内存
        __local__ float A_buf0[BLOCK_SIZE][BLOCK_SIZE];
        __local__ float A_buf1[BLOCK_SIZE][BLOCK_SIZE];
        __local__ float B_buf0[BLOCK_SIZE][BLOCK_SIZE];
        __local__ float B_buf1[BLOCK_SIZE][BLOCK_SIZE];
        __local__ float C_acc[BLOCK_SIZE][BLOCK_SIZE];
        
        for (int block_idx = start_block; block_idx < end_block; ++block_idx) {
            // 计算当前块的位置
            int block_i = (block_idx * BLOCK_SIZE) / N;
            int block_j = block_idx % (N / BLOCK_SIZE);
            int start_i = block_i * BLOCK_SIZE;
            int start_j = block_j * BLOCK_SIZE;
            
            // 初始化累加器
            for (int i = 0; i < BLOCK_SIZE; ++i) {
                for (int j = 0; j < BLOCK_SIZE; j += VECTOR_SIZE) {
                    float8 zeros = {0.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f, 0.0f};
                    vstore8(zeros, 0, &C_acc[i][j]);
                }
            }
            
            int current_buffer = 0;
            
            // 预加载第一个K块
            if (K > 0) {
                load_A_block(A_buf0, A_gm, start_i, 0, M, K, N);
                load_B_block(B_buf0, B_gm, 0, start_j, K, N, M);
            }
            
            // 分块计算
            for (int k_block = 0; k_block < K; k_block += BLOCK_SIZE) {
                int next_k_block = k_block + BLOCK_SIZE;
                
                // 异步预加载下一个块
                if (next_k_block < K) {
                    __local__ float* next_A = (current_buffer == 0) ? A_buf1 : A_buf0;
                    __local__ float* next_B = (current_buffer == 0) ? B_buf1 : B_buf0;
                    
                    load_A_block_async(next_A, A_gm, start_i, next_k_block, M, K, N);
                    load_B_block_async(next_B, B_gm, next_k_block, start_j, K, N, M);
                }
                
                // 等待当前块数据就绪
                __sync_buffers();
                
                // 获取当前缓冲区
                __local__ float* current_A = (current_buffer == 0) ? A_buf0 : A_buf1;
                __local__ float* current_B = (current_buffer == 0) ? B_buf0 : B_buf1;
                
                // 向量化矩阵乘法
                for (int i = 0; i < BLOCK_SIZE; ++i) {
                    for (int j = 0; j < BLOCK_SIZE; j += VECTOR_SIZE) {
                        float8 c_vec = vload8(0, &C_acc[i][j]);
                        
                        for (int k = 0; k < BLOCK_SIZE; ++k) {
                            float8 a_vec = float8(current_A[i][k]);
                            float8 b_vec = vload8(0, &current_B[k][j]);
                            c_vec += a_vec * b_vec;
                        }
                        
                        vstore8(c_vec, 0, &C_acc[i][j]);
                    }
                }
                
                // 切换缓冲区
                current_buffer = 1 - current_buffer;
            }
            
            // 写回结果
            store_C_block(C_acc, C_gm, start_i, start_j, M, N);
        }
    }
    
private:
    void load_A_block(__local__ float* dest, GM_ADDR src, 
                     int start_i, int start_k, int M, int K, int N) {
        for (int i = 0; i < BLOCK_SIZE; ++i) {
            for (int k = 0; k < BLOCK_SIZE; k += VECTOR_SIZE) {
                int global_i = start_i + i;
                int global_k = start_k + k;
                if (global_i < M && global_k < K) {
                    float8 data = vload8(0, ((float*)src) + global_i * K + global_k);
                    vstore8(data, 0, &dest[i * BLOCK_SIZE + k]);
                }
            }
        }
    }
};

第三章 高级优化技术与性能分析

3.1 内存访问优化

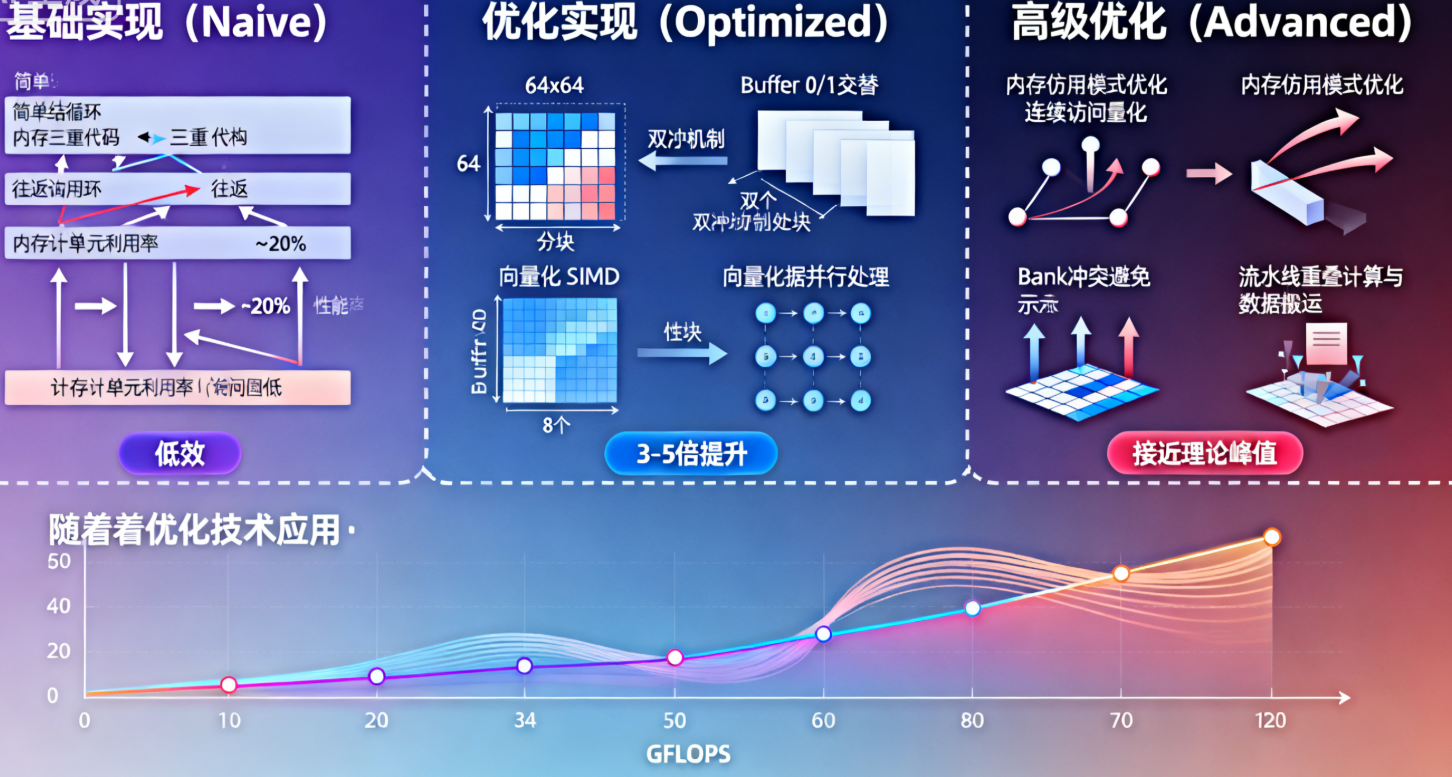
内存访问优化是矩阵乘性能提升的关键。在Ascend C中，我们可以通过多种手段优化内存访问：

• 数据布局优化：选择适合硬件架构的数据排列方式。对于矩阵乘法，通常建议使用行优先存储，但具体选择需要结合硬件特性和访问模式。
• 缓存友好访问：通过分块技术确保数据在缓存中有效重用。理想的分块大小应该使数据块能够完全容纳在本地内存中，减少全局内存访问。

// 缓存优化的数据加载
class CacheOptimizedLoader {
public:
    static void load_tile_with_prefetch(__local__ float* tile, 
                                      GM_ADDR src, 
                                      int row, int col,
                                      int ld, int tile_size) {
        // 预取数据
        prefetch_to_local(src + row * ld + col, tile_size * sizeof(float));
        
        // 异步加载
        for (int i = 0; i < tile_size; i += 8) {
            float8 data = vload8(0, ((float*)src) + (row + i) * ld + col);
            vstore8_async(data, 0, &tile[i * tile_size]);
        }
    }
};

Bank冲突避免：在并行访问共享内存时，确保不同线程访问不同的内存bank。可以通过调整数据布局或访问模式来消除冲突。

3.2 计算资源优化

计算资源优化关注如何充分利用AI Core的计算能力：

向量化计算：使用SIMD指令同时处理多个数据元素。Ascend C提供了丰富的向量内在函数支持。

// 向量化矩阵乘核心
class VectorizedCompute {
public:
    static void matmul_vectorized(__local__ float* A, 
                                __local__ float* B,
                                __local__ float* C,
                                int size) {
        for (int i = 0; i < size; ++i) {
            for (int j = 0; j < size; j += 8) {
                float8 c_vec = vload8(0, &C[i * size + j]);
                
                for (int k = 0; k < size; ++k) {
                    float8 a_vec = float8(A[i * size + k]);
                    float8 b_vec = vload8(0, &B[k * size + j]);
                    c_vec = __builtin_fma(a_vec, b_vec, c_vec);
                }
                
                vstore8(c_vec, 0, &C[i * size + j]);
            }
        }
    }
};

指令级并行：通过循环展开和软件流水线技术提高指令级并行度。

计算强度提升：增加每个内存访问对应的浮点操作数，提高计算内存比。

3.3 性能分析与调优

性能分析是优化的基础。我们需要建立科学的性能评估体系：

// 性能分析工具类
class Profiler {
private:
    uint64_t start_time;
    uint64_t total_cycles;
    uint64_t memory_cycles;
    
public:
    void start_measure() {
        start_time = get_cycle_count();
    }
    
    void end_measure(const char* section) {
        uint64_t end_time = get_cycle_count();
        uint64_t duration = end_time - start_time;
        total_cycles += duration;
        
        printf("Section %s: %lu cycles\n", section, duration);
    }
    
    void analyze_performance(int M, int N, int K) {
        double gflops = (2.0 * M * N * K) / (total_cycles * 1e-3);
        double memory_bw = ((M * K + K * N + M * N) * sizeof(float)) / 
                          (memory_cycles * 1e-3);
        
        printf("Performance: %.2f GFLOPS, Memory BW: %.2f GB/s\n", 
               gflops, memory_bw);
    }
};

第四章 实际应用与高级特性

4.1 批处理矩阵乘法

在实际AI应用中，经常需要处理批量矩阵乘法：

class BatchedMatMul {
public:
    __global__ __aicore__ void batched_matmul_kernel(
        uint32_t blockDim, uint32_t l2ctrl, uint32_t buffer, uint32_t length,
        int32_t batch_size, int32_t M, int32_t N, int32_t K) {
        
        uint32_t task_id = get_task_id();
        uint32_t task_num = get_task_num();
        
        // 计算每个任务处理的batch数
        int32_t batches_per_task = (batch_size + task_num - 1) / task_num;
        int32_t start_batch = task_id * batches_per_task;
        int32_t end_batch = min(start_batch + batches_per_task, batch_size);
        
        GM_ADDR A_gm = GET_GLOBAL_BUFFER(buffer);
        GM_ADDR B_gm = A_gm + batch_size * M * K * sizeof(float);
        GM_ADDR C_gm = B_gm + batch_size * K * N * sizeof(float);
        
        for (int batch = start_batch; batch < end_batch; ++batch) {
            GM_ADDR A_batch = A_gm + batch * M * K * sizeof(float);
            GM_ADDR B_batch = B_gm + batch * K * N * sizeof(float);
            GM_ADDR C_batch = C_gm + batch * M * N * sizeof(float);
            
            // 调用单矩阵乘法
            optimized_matmul_kernel(blockDim, l2ctrl, (uint32_t)A_batch, 
                                   M * K * sizeof(float), M, N, K);
        }
    }
};

4.2 支持不同数据类型的矩阵乘法

现代AI计算需要支持多种数据类型：

template<typename T>
class TypedMatMul {
public:
    __global__ __aicore__ void typed_matmul_kernel(
        uint32_t blockDim, uint32_t l2ctrl, uint32_t buffer, uint32_t length,
        int32_t M, int32_t N, int32_t K) {
        
        // 类型特定的优化策略
        if constexpr (sizeof(T) == 2) {
            // FP16优化策略
            optimize_for_fp16();
        } else if constexpr (sizeof(T) == 4) {
            // FP32优化策略
            optimize_for_fp32();
        }
        
        // 通用的矩阵乘法逻辑
        // ...
    }
    
private:
    void optimize_for_fp16() {
        // FP16特定的优化，如使用张量核心
        use_tensor_cores_if_available();
    }
    
    void optimize_for_fp32() {
        // FP32优化策略
        optimize_vectorization();
    }
};

第五章 完整测试与验证框架

5.1 测试框架实现

完整的测试框架确保算子正确性和性能：

class MatMulTestFramework {
public:
    struct TestConfig {
        int M, N, K;
        int batch_size;
        DataType dtype;
        bool verify_correctness;
        int num_iterations;
    };
    
    struct TestResult {
        double avg_time_ms;
        double max_error;
        double gflops;
        bool passed;
    };
    
    TestResult run_test(const TestConfig& config) {
        // 准备测试数据
        auto [A, B, C_expected] = generate_test_data(config);
        
        // 分配设备内存
        auto [A_dev, B_dev, C_dev] = allocate_device_memory(config);
        
        // 拷贝数据到设备
        copy_to_device(A, B, A_dev, B_dev);
        
        // 执行测试
        auto timings = run_kernel_multiple_times(config, A_dev, B_dev, C_dev);
        
        // 拷贝结果回主机
        auto C_result = copy_from_device(C_dev, config);
        
        // 验证正确性
        bool correct = verify_correctness(C_expected, C_result, config);
        
        // 计算性能指标
        double gflops = calculate_gflops(config, timings);
        
        return {calculate_average(timings), 
                calculate_max_error(C_expected, C_result),
                gflops, correct};
    }
    
private:
    std::tuple<std::vector<float>, std::vector<float>, std::vector<float>>
    generate_test_data(const TestConfig& config) {
        std::vector<float> A(config.M * config.K);
        std::vector<float> B(config.K * config.N);
        std::vector<float> C_expected(config.M * config.N);
        
        // 生成随机测试数据
        std::random_device rd;
        std::mt19937 gen(rd());
        std::uniform_real_distribution<float> dis(-1.0f, 1.0f);
        
        for (auto& val : A) val = dis(gen);
        for (auto& val : B) val = dis(gen);
        
        // 计算参考结果
        compute_reference_matmul(A, B, C_expected, config);
        
        return {A, B, C_expected};
    }
    
    bool verify_correctness(const std::vector<float>& expected,
                          const std::vector<float>& actual,
                          const TestConfig& config) {
        double max_error = 0.0;
        for (size_t i = 0; i < expected.size(); ++i) {
            double error = std::abs(expected[i] - actual[i]);
            max_error = std::max(max_error, error);
            
            if (error > config.tolerance) {
                std::cout << "Error at index " << i << ": expected " 
                         << expected[i] << ", got " << actual[i] 
                         << " (error: " << error << ")" << std::endl;
                return false;
            }
        }
        
        std::cout << "Verification passed. Max error: " << max_error << std::endl;
        return true;
    }
};

5.2 性能基准测试

建立全面的性能基准测试体系：

class BenchmarkSuite {
public:
    void run_comprehensive_benchmark() {
        std::vector<TestConfig> test_cases = {
            // 小矩阵测试
            {128, 128, 128, 1, FP32, true, 100},
            {256, 256, 256, 1, FP32, true, 50},
            
            // 中等矩阵测试
            {512, 512, 512, 1, FP32, true, 20},
            {1024, 1024, 1024, 1, FP32, true, 10},
            
            // 大矩阵测试
            {2048, 2048, 2048, 1, FP32, true, 5},
            {4096, 4096, 4096, 1, FP32, true, 2},
            
            // 批处理测试
            {256, 256, 256, 16, FP32, true, 10},
            {512, 512, 512, 8, FP32, true, 5}
        };
        
        MatMulTestFramework framework;
        for (const auto& config : test_cases) {
            auto result = framework.run_test(config);
            log_result(config, result);
            analyze_performance(config, result);
        }
    }
    
private:
    void analyze_performance(const TestConfig& config, const TestResult& result) {
        double theoretical_peak = get_theoretical_peak();
        double efficiency = (result.gflops / theoretical_peak) * 100.0;
        
        std::cout << "Matrix " << config.M << "x" << config.K << " * " 
                  << config.K << "x" << config.N << ": " << result.gflops 
                  << " GFLOPS (" << efficiency << "% of peak)" << std::endl;
    }
};

        通过这个完整的开发框架，我们可以系统地开发、测试和优化矩阵乘自定义算子，确保其在昇腾AI处理器上达到最佳性能。这种系统化的开发方法不仅适用于矩阵乘法，也可以推广到其他类型的自定义算子开发中。

2025年昇腾CANN训练营第二季，基于CANN开源开放全场景，推出0基础入门系列、码力全开特辑、开发者案例等专题课程，助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证，即可领取精美证书，完成社区任务更有机会赢取华为手机，平板、开发板等大奖。

报名链接：https://www.hiascend.com/developer/activities/cann20252