Ascend C融合算子开发全攻略:原理、实现与性能优化详解
第一章:融合算子技术概述与理论基础
1.1 融合算子的概念与重要性
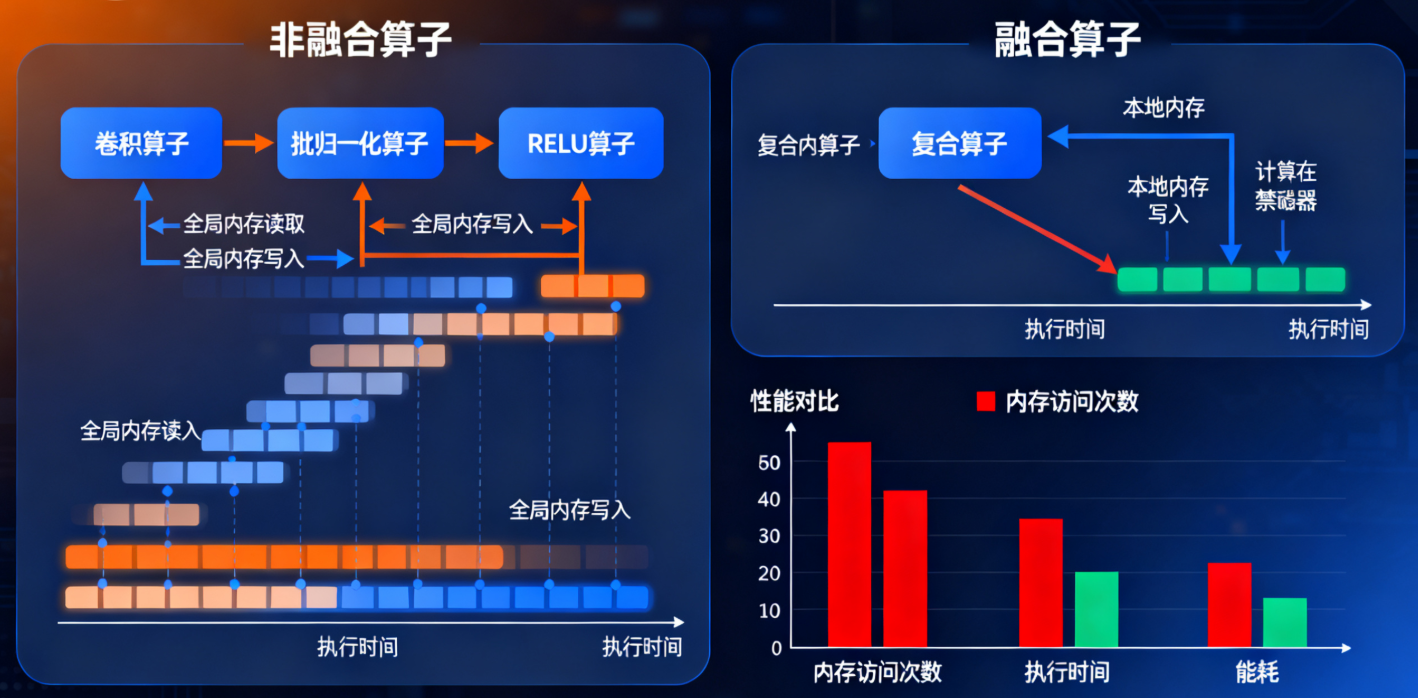
在AI计算领域,融合算子(Kernel Fusion)是一项关键的性能优化技术,它通过将多个基本算子组合成单一的复合算子,显著提升计算效率。传统AI模型中,每个算子都需要独立的内存读写操作,而融合算子技术能够有效减少这种内存访问开销。
融合算子的核心价值体现在三个层面:首先,它通过减少中间结果的存储和读取,大幅降低内存带宽需求;其次,多个操作的融合执行减少了核函数启动开销;最后,它提供了更好的数据局部性,使得计算更加高效。
从硬件架构角度看,昇腾AI处理器采用达芬奇架构,其计算单元、存储系统和控制单元的协同工作模式特别适合融合算子的执行。当多个相关操作在同一个核函数中连续执行时,数据可以保留在高速的本地内存中,避免频繁的全局内存访问,从而充分发挥硬件性能。
1.2 融合算子的技术分类
根据融合的粒度和方式,我们可以将融合算子分为以下几种类型:
- 垂直融合(Vertical Fusion):将模型中连续的多个层或操作融合在一起。例如将卷积、批归一化、激活函数三个连续操作融合为一个复合算子。这种融合方式最常用,收益也最明显。
- 水平融合(Horizontal Fusion):将并行执行的多个相同或相似操作融合在一起。比如将多个分支的卷积操作融合,同时处理多条计算路径。
- 对角线融合(Diagonal Fusion):结合垂直和水平融合的混合模式,适用于复杂的网络结构如ResNet、Inception等。
- 特定模式融合:针对特定计算模式的优化融合,如Attention机制中的QKV计算融合,或者Transformer块中的特定操作序列融合。
1.3 融合算子的性能收益分析
融合算子的性能提升主要来自以下几个方面:
- 内存访问优化:这是最主要的收益来源。以"卷积+ReLU"融合为例,非融合情况下,卷积结果需要写入全局内存,然后ReLU再读取这些数据。融合后,中间结果保留在寄存器或本地内存中,节省了两次内存传输。
- 核函数启动开销减少:每个核函数的启动都有固定的开销,包括参数传递、资源分配等。融合多个操作意味着减少核函数调用次数。
- 数据局部性提升:连续操作的数据可以更好地利用缓存,减少缓存失效的情况。
- 并行度优化:融合算子可以更好地平衡计算负载,避免某些核函数过轻或过重的负载不均问题。
理论分析表明,在合适的场景下,融合算子可以实现30%-300%不等的性能提升,具体收益取决于原始算子的计算内存比、数据重用程度等因素。
第二章:Ascend C融合算子开发环境与工具链
2.1 开发环境配置详解
Ascend C融合算子的开发需要完整的环境支持,包括硬件环境、软件栈和开发工具。首先需要确保CANN(Compute Architecture for Neural Networks)工具包的正确安装和配置。
环境验证步骤:
# 检查CANN环境
source /usr/local/Ascend/ascend-toolkit/set_env.sh
ascend-check --version
# 验证AI处理器状态
npu-smi info
# 检查编译环境
aarch64-linux-gnu-gcc --version关键环境变量配置:
export ASCEND_HOME=/usr/local/Ascend/ascend-toolkit/latest
export PATH=${ASCEND_HOME}/bin:${PATH}
export LD_LIBRARY_PATH=${ASCEND_HOME}/lib64:${LD_LIBRARY_PATH}
export ASCEND_OPP_PATH=${ASCEND_HOME}/opp
export PYTHONPATH=${ASCEND_HOME}/python/site-packages:${PYTHONPATH}2.2 融合算子开发工具链
Ascend平台提供了一套完整的融合算子开发工具,主要包括:
- Ascend Compiler:负责将高级别算子描述编译为可在AI Core上执行的二进制代码,支持自动优化和流水线调度。
- Ascend Graph Engine:提供图级别的优化和融合机会发现,能够自动识别可融合的算子模式。
- Profiling Tools:性能分析工具,帮助开发者识别性能瓶颈,指导融合策略的选择。
- Debugging Tools:调试工具集,支持核函数的单步调试、内存访问检查等功能。
- 模板代码生成器:自动生成融合算子的基础代码框架,大幅减少开发工作量。
2.3 开发流程与方法论
成功的融合算子开发需要遵循系统化的流程:
- 需求分析阶段:明确融合目标,分析原始算子的计算模式、数据流和性能特征。
- 设计阶段:制定融合策略,确定数据布局、内存访问模式和计算调度方案。
- 实现阶段:编写核函数代码,注重代码的可读性和可维护性。
- 调试优化阶段:通过性能分析工具识别瓶颈,迭代优化实现。
- 验证阶段:确保功能正确性,验证数值精度和边界条件处理。
第三章:典型融合算子模式分析与实现
3.1 卷积-批归一化-激活函数融合
这是深度学习中最常见的融合模式之一,在卷积神经网络中广泛应用。
技术难点分析:
-
三个算子的数据布局可能不一致
-
批归一化的均值和方差需要特殊处理
-
激活函数的原位操作限制
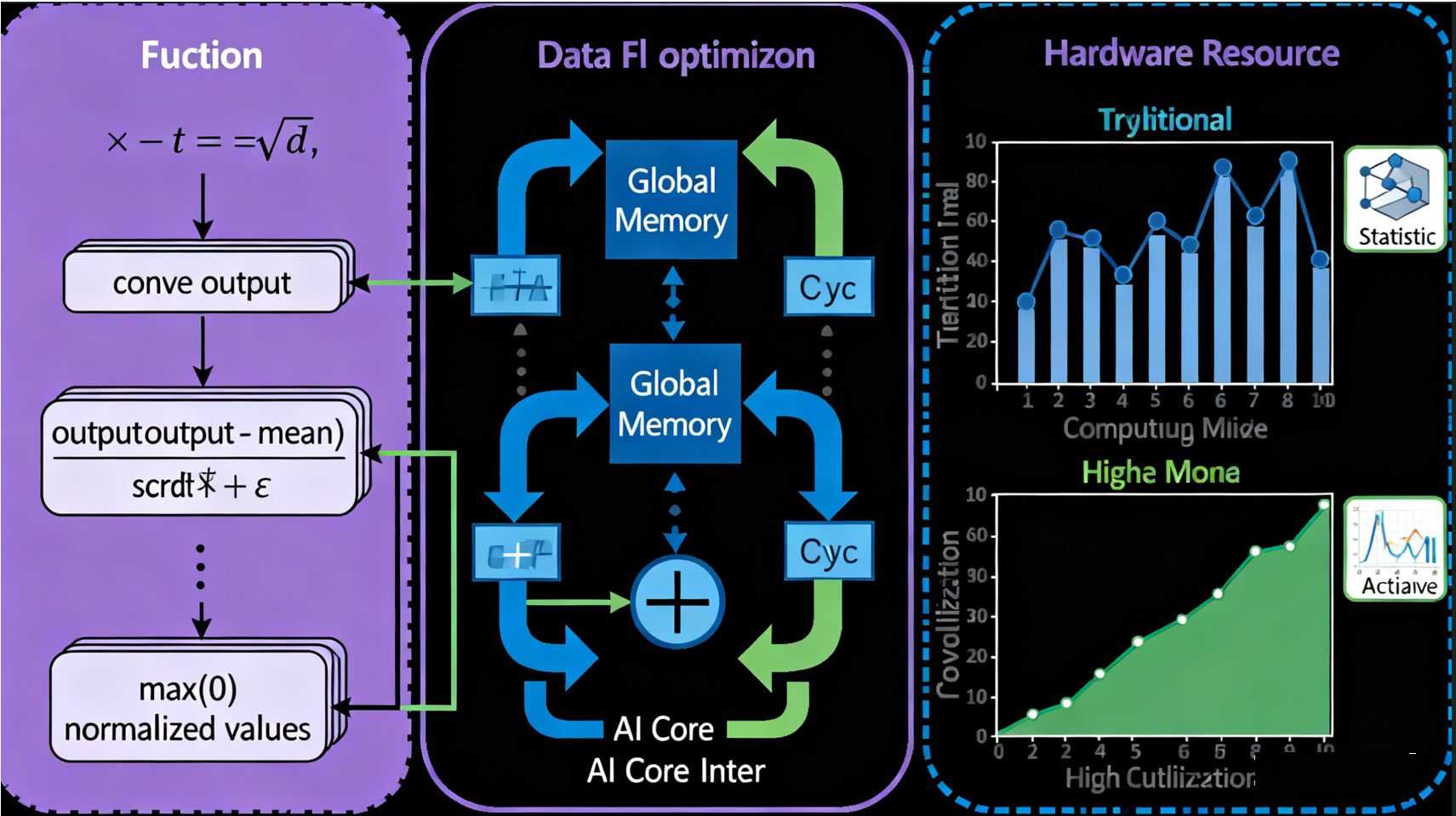
融合实现策略:
class ConvBatchNormReluFusion {
private:
// 卷积参数
int in_channels_, out_channels_, kernel_size_;
// 批归一化参数
float epsilon_, scale_, bias_;
public:
// 融合核函数
__global__ __aicore__ void fused_conv_bn_relu_kernel(
const float* input, const float* weight,
const float* running_mean, const float* running_var,
float* output, int batch_size, int height, int width) {
// 计算任务划分
int task_id = get_task_id();
int total_tasks = get_task_num();
// 每个任务处理的输出通道数
int channels_per_task = (out_channels_ + total_tasks - 1) / total_tasks;
int start_channel = task_id * channels_per_task;
int end_channel = min(start_channel + channels_per_task, out_channels_);
// 本地内存分配
__local__ float input_tile[TILE_SIZE][TILE_SIZE];
__local__ float weight_tile[KERNEL_TILE][KERNEL_TILE];
__local__ float output_tile[TILE_SIZE][TILE_SIZE];
for (int b = 0; b < batch_size; ++b) {
for (int h = 0; h < height; h += TILE_SIZE) {
for (int w = 0; w < width; w += TILE_SIZE) {
// 数据搬运:输入和权重的分块加载
load_input_tile(input, input_tile, b, h, w);
load_weight_tile(weight, weight_tile, start_channel);
// 卷积计算
convolution_2d(input_tile, weight_tile, output_tile);
// 批归一化融合
for (int i = 0; i < TILE_SIZE; ++i) {
for (int j = 0; j < TILE_SIZE; ++j) {
// BN计算:output = (conv_output - mean) / sqrt(var + epsilon) * scale + bias
float bn_output = (output_tile[i][j] - running_mean[start_channel]) *
rsqrt(running_var[start_channel] + epsilon_) * scale_ + bias_;
// ReLU激活融合
output_tile[i][j] = max(0.0f, bn_output);
}
}
// 结果写回
store_output_tile(output, output_tile, b, h, w, start_channel);
}
}
}
}
};性能优化要点:
-
使用双缓冲技术重叠计算和数据传输
-
合理安排数据布局以减少bank冲突
-
利用向量化指令加速批归一化计算
-
优化循环展开策略提高指令级并行
3.2 LayerNorm-GeLU融合算子
在Transformer类模型中,LayerNorm后接GeLU激活是常见模式,这种融合可以显著提升性能。
数学公式分析:
LayerNorm: y=Var[x]+ϵx−E[x]×γ+β
GeLU: GeLU(x)=0.5x×(1+tanh(π2×(x+0.044715x3)))
融合实现代码:
class LayerNormGeLUFusion {
public:
static constexpr int VECTOR_SIZE = 64;
static constexpr float GELU_COEF = 0.044715f;
static constexpr float SQRT_2_OVER_PI = 0.7978845608028654f;
__global__ __aicore__ void fused_layernorm_gelu_kernel(
const half* input, half* output,
const half* gamma, const half* beta,
float epsilon, int seq_len, int hidden_size) {
int task_id = get_task_id();
int total_tasks = get_task_num();
// 计算任务划分:每个任务处理连续的hidden_size维度
int elements_per_task = (hidden_size + total_tasks - 1) / total_tasks;
int start_idx = task_id * elements_per_task;
int end_idx = min(start_idx + elements_per_task, hidden_size);
__local__ half local_input[VECTOR_SIZE];
__local__ half local_output[VECTOR_SIZE];
__local__ float mean_accum, var_accum;
for (int seq = 0; seq < seq_len; ++seq) {
// 阶段1:计算均值和方差
mean_accum = 0.0f;
var_accum = 0.0f;
for (int i = start_idx; i < end_idx; i += VECTOR_SIZE) {
int valid_size = min(VECTOR_SIZE, end_idx - i);
__memcpy_async(local_input, input + seq * hidden_size + i,
valid_size * sizeof(half));
// 向量化计算均值和方差
float4 vec_mean = float4(0.0f);
for (int j = 0; j < valid_size; j += 4) {
float4 vals = float4(local_input[j], local_input[j+1],
local_input[j+2], local_input[j+3]);
vec_mean += vals;
}
mean_accum += (vec_mean.x + vec_mean.y + vec_mean.z + vec_mean.w);
}
float mean = mean_accum / hidden_size;
// 计算方差
for (int i = start_idx; i < end_idx; i += VECTOR_SIZE) {
int valid_size = min(VECTOR_SIZE, end_idx - i);
__memcpy_async(local_input, input + seq * hidden_size + i,
valid_size * sizeof(half));
float4 vec_var = float4(0.0f);
for (int j = 0; j < valid_size; j += 4) {
float4 vals = float4(local_input[j], local_input[j+1],
local_input[j+2], local_input[j+3]);
float4 diff = vals - float4(mean);
vec_var += diff * diff;
}
var_accum += (vec_var.x + vec_var.y + vec_var.z + vec_var.w);
}
float variance = var_accum / hidden_size;
float inv_std = rsqrt(variance + epsilon);
// 阶段2:LayerNorm + GeLU融合计算
for (int i = start_idx; i < end_idx; i += VECTOR_SIZE) {
int valid_size = min(VECTOR_SIZE, end_idx - i);
__memcpy_async(local_input, input + seq * hidden_size + i,
valid_size * sizeof(half));
for (int j = 0; j < valid_size; ++j) {
// LayerNorm计算
float normalized = (local_input[j] - mean) * inv_std * gamma[i+j] + beta[i+j];
// GeLU近似计算(使用tanh近似)
float x = normalized;
float x_cube = x * x * x;
float inner = SQRT_2_OVER_PI * (x + GELU_COEF * x_cube);
float gelu = 0.5f * x * (1.0f + tanh(inner));
local_output[j] = __float2half(gelu);
}
__memcpy_async(output + seq * hidden_size + i, local_output,
valid_size * sizeof(half));
}
}
}
};第四章:融合算子性能优化高级技巧
4.1 内存访问模式优化
内存访问效率是融合算子性能的关键因素。优化内存访问需要从多个层面考虑:
- 数据布局优化:选择最适合硬件架构的数据排列方式。对于Ascend AI处理器,建议使用NHWC格式,这种格式更适合向量化操作,能够提供更好的空间局部性。
- 缓存友好访问:通过数据分块技术确保数据在缓存中有效重用。合理的分块大小应该考虑多级缓存容量,避免不必要的缓存失效。
- bank冲突避免:在并行访问共享内存时,确保不同线程访问不同的内存bank。可以通过调整数据布局或访问偏移来消除bank冲突。
- 预取技术应用:在计算当前数据块的同时,预取下一个数据块到本地内存,隐藏内存访问延迟。
4.2 计算资源优化策略
计算资源的有效利用直接影响融合算子的性能:
- 指令级并行优化:通过循环展开、软件流水线等技术提高指令级并行度。Ascend C编译器支持自动向量化,但手动优化往往能获得更好效果。
- 计算强度提升:增加每个内存访问对应的计算操作数,提高计算内存比。这对于内存带宽受限的操作特别重要。
- 特殊函数近似:对于复杂的数学函数如指数、对数、三角函数等,使用硬件优化的近似实现,在精度可接受的范围内提升性能。
- 混合精度计算:在适当场景下使用FP16、BF16等低精度格式,利用硬件对低精度计算的高效支持。
4.3 并行度与负载均衡
有效的并行策略是发挥硬件性能的关键:
- 多层次并行:结合任务级并行、数据级并行和指令级并行,形成立体的并行计算结构。
- 动态负载均衡:根据数据特征动态调整任务分配,避免某些处理单元过载而其他单元空闲的情况。
- 资源感知调度:考虑内存带宽、计算单元、存储容量等资源约束,制定最优的调度策略。
第五章:融合算子调试与性能分析
5.1 调试方法与工具使用
融合算子的调试比单个算子更复杂,需要系统化的调试方法:
- 分层调试策略:首先验证单个组件的正确性,然后逐步组合验证整体功能。这种自底向上的方法可以快速定位问题。
- 数值精度验证:建立完整的数值验证框架,对比融合算子与原始算子序列的结果差异,确保数值精度在可接受范围内。
- 边界条件测试:特别关注各种边界情况,如零值输入、极端值、特殊形状等,确保算子的鲁棒性。
- 内存访问检查:使用Ascend平台提供的内存检查工具,检测越界访问、未初始化内存等问题。
5.2 性能分析与优化指导
性能分析是优化工作的基础,需要科学的方法论:
- 性能瓶颈定位:使用Ascend Profiler工具分析计算、内存、通信等各个方面的性能数据,识别主要瓶颈。
- 关键指标监控:重点关注计算利用率、内存带宽利用率、缓存命中率等关键性能指标。
- 优化效果评估:建立科学的基准测试框架,准确评估每个优化措施的实际效果,避免无效优化。
- 自动化优化探索:对于复杂的参数空间,可以使用自动化工具探索最优配置,如分块大小、并行度等参数。
第六章:实际应用场景与案例分析
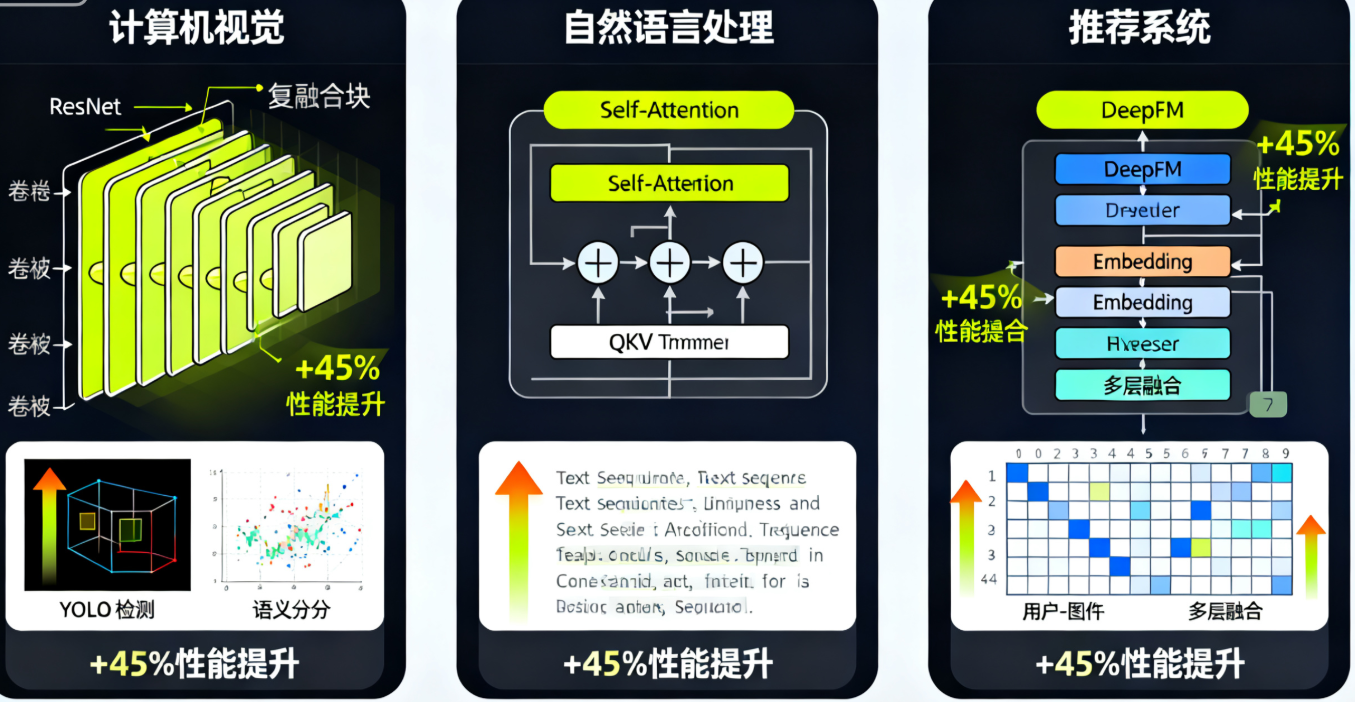
6.1 计算机视觉模型融合优化
在计算机视觉领域,卷积神经网络的融合优化具有重要价值:
- ResNet模型融合:针对残差连接的特殊结构,设计专门的融合策略。将卷积、批归一化、残差连接和激活函数融合为单一算子,减少中间结果存储。
- YOLO目标检测优化:针对YOLO的多尺度检测特性,设计跨尺度的融合计算模式,优化特征金字塔的计算效率。
- 语义分割模型优化:针对编码器-解码器结构,设计对称的融合计算模式,充分利用特征重用。
6.2 自然语言处理模型优化
Transformer架构为融合算子提供了丰富的优化机会:
- Self-Attention融合:将QKV计算、注意力权重计算、softmax、权重应用等操作融合,显著减少内存访问。
- FFN层优化:将全连接层、激活函数、残差连接融合,提升前馈网络的计算效率。
- 跨层优化:识别Transformer块间的融合机会,设计跨多个层的复合融合算子。
6.3 推荐系统模型优化
推荐系统模型具有独特的计算特征,需要专门的融合策略:
- Embedding层融合:将多个Embedding查找操作融合,提高内存访问效率。
- 多层级融合:针对Wide&Deep、DeepFM等复杂模型,设计端到端的融合计算图。
- 动态形状优化:推荐系统输入形状多变,需要设计适应性强的融合策略。
第七章:未来发展趋势与挑战
7.1 技术发展趋势
融合算子技术正在向更智能、更自动化的方向发展:
- AI驱动的自动融合:利用机器学习技术自动发现融合机会,生成优化的融合策略,减少人工参与。
- 跨平台融合:支持在异构计算平台上自动生成优化的融合代码,提高代码可移植性。
- 动态融合:根据运行时信息动态调整融合策略,适应不同的输入特性和硬件状态。
- 领域特定融合:针对特定应用领域(如科学计算、图形处理等)设计专门的融合模式。
7.2 面临的挑战与解决方案
融合算子技术发展仍面临诸多挑战:
- 通用性与特殊性平衡:如何在保持通用性的同时充分利用硬件特性,需要创新的架构设计。
- 开发复杂度管理:融合算子开发复杂度高,需要更好的开发工具和方法论支持。
- 验证与测试挑战:融合算子的正确性验证更加复杂,需要建立完善的验证体系。
- 性能可移植性:在不同硬件平台上保持性能一致性是重要挑战。
结语:掌握融合算子,开启AI计算新纪元
融合算子技术是提升AI计算效能的关键手段,通过本训练营的系统学习,我们深入探讨了融合算子的理论基础、开发方法、优化技巧和实践应用。从简单的算子组合到复杂的计算图优化,融合算子技术为AI计算性能提升提供了系统化的解决方案。
作为AI计算开发者,掌握融合算子技术不仅能够提升模型性能,更重要的是培养了系统级的优化思维。这种思维模式将帮助我们在面对新的计算挑战时,能够从整体架构角度出发,制定最优的解决方案。
未来,随着AI模型的不断演进和硬件架构的持续创新,融合算子技术将发挥越来越重要的作用。希望本训练营的内容能够为您的AI计算优化之旅提供坚实的理论基础和实践指导,助力您在AI计算领域取得更大成就。
继续学习建议:
-
深入阅读Ascend C官方文档和最佳实践指南
-
参与开源社区项目,积累实际项目经验
-
关注最新研究进展,持续学习新的优化技术
-
建立性能分析习惯,培养数据驱动的优化思维
融合算子技术的掌握是一个持续学习、不断实践的过程。希望通过本训练营的学习,您已经建立了坚实的技术基础,能够在实际工作中灵活运用这些知识,为AI计算效能提升做出重要贡献。
2025年昇腾CANN训练营第二季,基于CANN开源开放全场景,推出0基础入门系列、码力全开特辑、开发者案例等专题课程,助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证,即可领取精美证书,完成社区任务更有机会赢取华为手机,平板、开发板等大奖。
报名链接:https://www.hiascend.com/developer/activities/cann20252
更多推荐
 已为社区贡献4条内容
已为社区贡献4条内容









所有评论(0)