CANN算子开发深度解析：从基础矩阵乘法到极致性能优化

引言

在深度学习领域，矩阵乘法（MatMul）是最基础、也是最关键的操作之一。无论是 Transformer 的注意力机制、传统的全连接网络，还是卷积操作的底层实现，都绕不开高性能的矩阵运算。在昇腾 NPU 上开发一个高效 MatMul 算子并不是简单地把数学公式翻译成代码，而是要充分理解计算密度、内存带宽、硬件单元以及数据流调度等多维因素。

本文将以 CANN（Compute Architecture for Neural Networks）为分析框架，结合昇腾 NPU 的 Cube 单元特点，从算法结构到硬件调度逐层拆解 MatMul 算子的优化路径。无论你是算子开发新手还是准备冲击 Ascend C 认证的进阶开发者，都可以通过本文建立体系化的性能优化思路。

---

训练营简介

2025年昇腾CANN训练营第二季，基于CANN开源开放全场景，推出0基础入门系列、码力全开特辑、开发者案例等专题课程，助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证，即可领取精美证书，完成社区任务更有机会赢取华为手机，平板、开发板等大奖。

报名链接：https://www.hiascend.com/developer/activities/cann20252#cann-camp-2502-intro

一、MatMul算子的问题本质：高计算密度与高访存压力并存

1.1 计算复杂度的暴力增长

标准矩阵乘法 C = A × B，其中 A 维度为 M×K，B 为 K×N，对应的计算复杂度为：

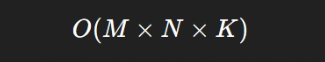
当 M=N=K=1024 时，需要执行约 10⁹ 次浮点乘加。即使在高算力平台上，这仍然是一个可观的工作量。

关键瓶颈包括：

• 运算密度高，Cube 单元必须持续满负载
• 访存量大，L0/L1/Gm 的带宽约束会直接拉低性能
• 数据复用不足时，访存会成为主要阻力

1.2 昇腾 NPU 的硬件结构：性能的真正上限

昇腾 NPU 内部的 Cube 单元是面向矩阵运算设计的脉动阵列，特点包括：

• 单个 Cube 为 16×16 宏单元，天然适配矩阵块计算
• FP16 运算吞吐能力是 FP32 的约 2 倍
• 要求数据布局满足 16 对齐格式

对于 MatMul 来说，能否让 Cube 单元持续“吃满”，决定了最终能达到多少峰值算力占比。

---

二、基础实现往往性能惨烈：为什么朴素版本跑不快？

一个新手最容易写出的 MatMul 算子一般如下路径：

1. 从 GM 直接读 A、B
2. 直接在 L1 执行循环乘加
3. 把结果写回 GM

这样做性能非常低，因为：

• 访存没有 Tiling，访问跨度过大，缓存无法命中
• 计算阶段和搬运阶段完全串行
• 缺乏数据重用，同一块数据被反复从 GM 读取
• 没有根据 Cube 特性对齐数据格式

实测可能只有 20%～30% 的峰值算力。

因此，优化必须系统化推进。

---

三、Tiling：MatMul 性能优化的第一道分水岭

3.1 为什么必须 Tiling？

昇腾 NPU 的 L0 缓存容量有限，不可能一次性给你 M×K、K×N 的完整矩阵。为了让局部块可以复用，就必须把大矩阵分成小块处理。

目的有三个：

1. 减少 GM ↔ L1 的访存压力
2. 提高数据的重复利用率
3. 让块大小刚好符合 Cube 的最佳处理尺寸

3.2 Tiling 的设计约束

典型原则如下：

• Tile_M、Tile_N、Tile_K 必须是 16 的倍数，保证对齐 Cube

• 内部块需要满足：

• 尽可能增大 Tile 尺寸，使数据复用最大化

Tiling 的设计决定了后续 Pipeline 和计算调度的上限，是算子优化中至关重要的一步。

---

四、Pipeline：算子性能提升的“倍数器”

4.1 为什么需要流水线？

在无流水线模式下，执行流程为：

搬运 → 计算 → 写回

三者严格串行。Cube 单元经常在等待数据，而不是计算。

4.2 三级流水线结构

CANN 中典型的 MatMul 流水线分为：

1. CopyIn 阶段：预取 A 与 B 的块
2. Compute 阶段：Cube 单元执行 Tile 块的乘法
3. CopyOut 阶段：将结果写回 GM

当三个阶段并行交错执行时，可以达到理论加速比约 3。

实际工程中，因为存在边界条件与同步问题，一般可达到：

• 2～2.5 倍的有效加速

Pipeline 是 MatMul 性能提升最关键的优化手段之一。

---

五、内存访问优化：比计算更难的部分

5.1 Bank 冲突：隐藏的性能杀手

L0 缓存分成多个 Bank，如果访存模式不合理，多个线程会击中同一个 Bank，导致访问串行，性能急剧下降。

解决方法包括：

• 对矩阵数据加 padding
• 调整 Tiling 的内外循环顺序
• 使用 CANN 提供的 2D 数据搬运指令 来进行规则访问

5.2 数据重用策略：带宽节省的关键

对于 MatMul：

• A 的行要与 B 的列组合多次
• 某一 Tile 的数据往往可以被复用数十次

常见策略：

• A_block 重用多个 B_block
• B_block 重用多个 A_block
• 调整乘法顺序，使得 L1/L0 命中率最大化

通过重用设计，内存带宽利用率可从约 40% 提升到 70% 以上。

---

六、混合精度：精度与性能的黄金平衡

6.1 FP16 计算 + FP32 累加

一种常用方法：

1. A、B 数据以 FP16 存储
2. Cube 中使用 FP16 进行 FP16×FP16 乘法
3. 累加使用 FP32
4. 最终再输出到 FP16/FP32

优势：

• 接近 2 倍性能提升
• 保证数值误差 < 1e-3

6.2 INT8 量化：推理场景的“性能核武器”

量化流程包括：

1. 统计数据范围
2. 生成 scale/zero_point
3. 执行 INT8 Gemm
4. 反量化输出结果

INT8 MatMul 的吞吐通常为 FP32 的 3~4 倍，需要对量化噪声进行细致控制。

---

七、大规模矩阵的特殊优化：单机也要考虑分治与通信

当矩阵尺寸上升至 4096×4096、8192×8192 级别时，单块 Tiling 甚至 L1/L2 都无法满足需求。

优化包括：

7.1 分块策略（Blockwise MatMul）

• 外层将整个矩阵分成若干子矩阵
• 内层子矩阵继续走 Tiling + Pipeline
• 需要保证各核之间任务量均衡

7.2 多核通信优化

跨核通信成为瓶颈时，需要：

• 异步通信隐藏数据搬运开销
• 合理设计拓扑结构降低跨核数据量
• 使用 All-Reduce 等高效通信原语

针对多核场景的优化往往能提升 20～40% 的整体性能。

---

八、实测性能演进（示例）

这类优化通常会有类似的演变过程：

优化阶段	峰值占比	耗时（1024×1024）	提升倍数
初始朴素实现	25%	8.0 ms	1.0×
加入 Tiling	50%	4.0 ms	2.0×
开启 Pipeline	70%+	2.8 ms	2.8×
混合精度与全面调优	85%+	1.2 ms	6.7×

越往高处走，越需要体系化优化，而不是局部小修小补。

---

九、学习资源与社区生态

针对希望系统学习 CANN 算子开发的工程师，昇腾社区提供：

• CANN 训练营课程：包含基础理论、算子规范、样例项目
• 码力全开系列：从入门算子到高阶优化的案例拆解
• 真实企业案例对话室：深入分析推荐系统、大模型推理场景的算子实现
• Ascend C 认证体系：覆盖算子开发能力全链路的专业考试

通过系统训练，开发者可以快速掌握 CANN 体系下高性能算子开发的核心技能。

---

总结

MatMul 算子的优化不是单一技巧，而是横跨算法、硬件结构、调度、访存策略的一整套工程体系。本文从计算复杂度分析开始，依次介绍了：

• Tiling 设计
• Pipeline 并行
• 数据重用与 Bank 优化
• 混合精度与量化
• 大矩阵的分块和通信调度

掌握这些方法不仅能开发高性能 MatMul，也能迁移到卷积、归一化、注意力等其他高算子密度的场景中。

随着昇腾生态持续开放，CANN 对开发者的友好度和工具链成熟度不断提升。无论你是行业工程师、科研人员，还是准备参与大模型优化的开发者，高效算子开发都将成为未来 AI 计算工程的重要核心能力。