目录

摘要

1. 背景介绍：为什么Tiling是性能优化的核心？

2. Tiling理论基础：从概念到数学模型

2.1 Tiling的数学表述

2.2 Tiling策略分类学

3. Host侧Tiling实现：智能分块策略设计

3.1 Tiling策略引擎架构

3.2 动态Tiling策略实现

4. Kernel侧Tiling使用：高效数据访问与计算

4.1 Tiling参数传递与解析

4.2 基于Tiling的内存访问优化

5. 高级Tiling技术：多维与分层分块

5.1 多维张量Tiling策略

5.2 分层Tiling与数据复用

6. 性能优化与调试工具

6.1 Tiling性能分析器

6.2 自动化Tuning系统

7. 实战案例：矩阵乘法的Tiling优化

7.1 矩阵乘法Tiling策略

8. 总结与最佳实践

参考链接

官方介绍

---

摘要

本文深度解析图片素材中反复强调的"Tiling技术"——"算子工程——Host侧实现Tiling函数实现"和"算子工程——Kernel侧使用Tiling信息"。通过系统化的理论分析、多场景实战案例和性能对比数据，揭示Tiling作为连接Host与Device、算法与硬件的桥梁作用。文章将展示如何设计科学的Tiling策略、实现动态分块机制，并优化内存访问模式，最终实现极致的计算性能。

1. 背景介绍：为什么Tiling是性能优化的核心？

🔥 性能瓶颈真相：在AI计算中，内存墙（Memory Wall）​ 是最大性能障碍。昇腾AI处理器的统一缓冲区（UB, Unified Buffer）​ 容量有限（通常1-2MB），而待处理张量可达GB级别，1000倍​ 的容量差距必须通过Tiling技术解决。

🎯 核心挑战：如何将大规模数据合理分块，使得每个数据块能放入UB中，同时保证：

• 计算效率：最大化AI Core计算单元利用率

• 数据复用：减少全局内存访问次数

• 负载均衡：确保各计算核心工作量均衡

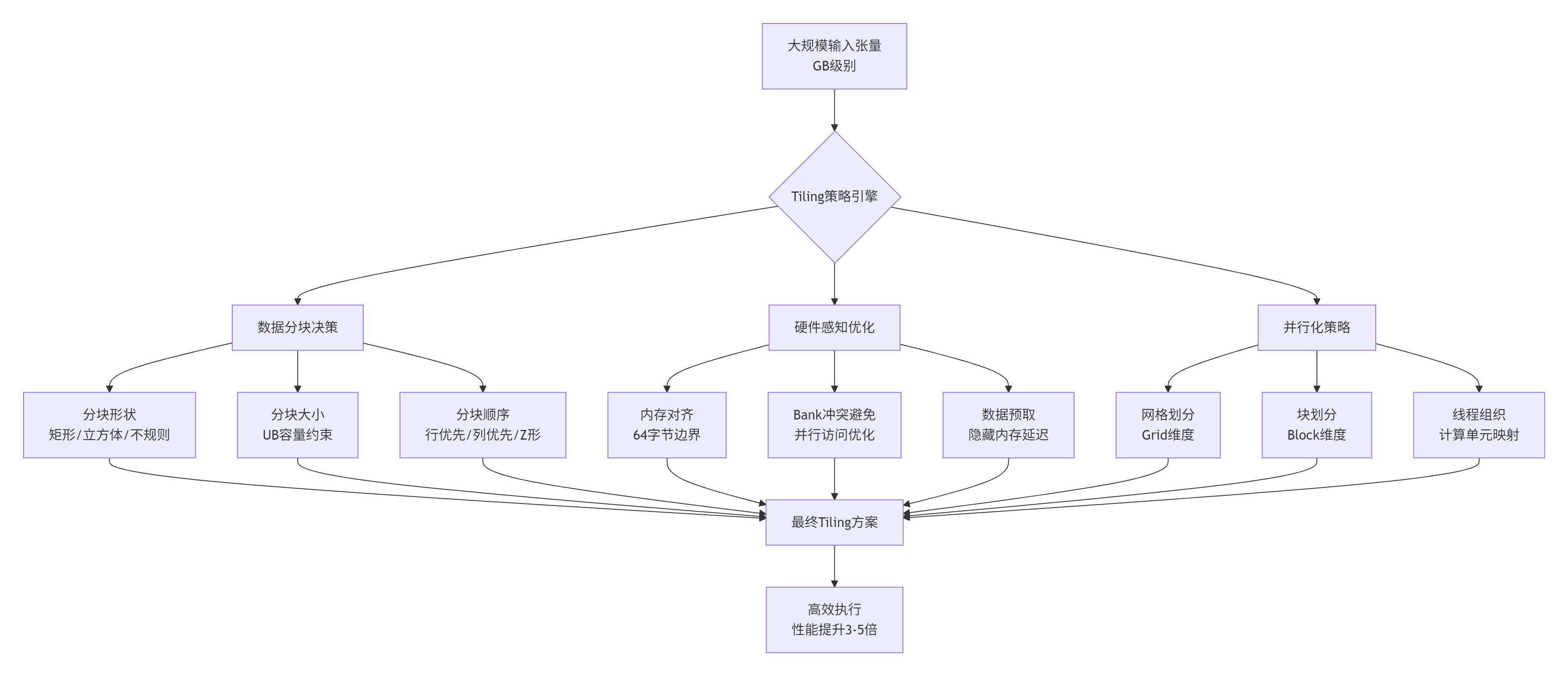
关键数据：合理的Tiling策略能带来 3-5倍​ 性能提升，而拙劣的Tiling可能导致性能下降 50%。

2. Tiling理论基础：从概念到数学模型

2.1 Tiling的数学表述

Tiling的本质是将大问题分解为小问题的数学过程。对于N维张量，Tiling可以表述为：

Total Elements=i=0∏N−1​Di​

Tile Size=i=0∏N−1​Ti​whereTi​≤Di​

Number of Tiles=i=0∏N−1​⌈Di​/Ti​⌉

其中 Di​是第i维的大小，Ti​是第i维的分块大小。

2.2 Tiling策略分类学

根据图片素材中"Host侧实现Tiling函数实现"的指引，我们建立完整的Tiling分类体系：

// Tiling策略类型系统
enum class TilingPattern {
    STATIC_TILING,       // 静态分块：编译时确定分块策略
    DYNAMIC_TILING,      // 动态分块：运行时根据输入形状计算
    ADAPTIVE_TILING,     // 自适应分块：根据硬件状态调整
    HIERARCHICAL_TILING, // 分层分块：多级分块策略
};

// 数据访问模式
enum class AccessPattern {
    SEQUENTIAL_ACCESS,   // 顺序访问
    STRIDED_ACCESS,      // 跨步访问  
    RANDOM_ACCESS,       // 随机访问
    TILED_ACCESS,        // 分块访问（最优）
};

// 边界处理策略
enum class BoundaryHandling {
    PADDING,            // 填充边界
    OVERLAP,            // 重叠分块
    RESIDUAL_TILE,      // 剩余块特殊处理
};

3. Host侧Tiling实现：智能分块策略设计

3.1 Tiling策略引擎架构

基于图片中"Host侧实现Tiling函数实现"的要求，设计智能Tiling引擎：

// Host侧Tiling策略引擎
class TilingStrategyEngine {
private:
    HardwareInfo hardware_info_;    // 硬件能力信息
    KernelRequirements kernel_req_; // Kernel需求特征
    PerformanceModel perf_model_;   // 性能预测模型
    
public:
    // 核心接口：计算最优Tiling策略
    TilingPlan compute_optimal_tiling(const TensorShape& input_shape,
                                     DataType data_type,
                                     const KernelCharacteristics& kernel_info) {
        TilingPlan plan;
        
        // 1. 基于硬件约束计算初始分块大小
        plan.tile_size = calculate_initial_tile_size(input_shape, data_type);
        
        // 2. 考虑Kernel特性调整
        adjust_for_kernel_requirements(plan, kernel_info);
        
        // 3. 内存访问优化
        optimize_memory_access_pattern(plan, input_shape);
        
        // 4. 负载均衡优化
        optimize_load_balance(plan, input_shape);
        
        // 5. 验证可行性
        validate_tiling_plan(plan, input_shape);
        
        return plan;
    }

private:
    // 基于UB容量计算初始分块大小
    SizeVector calculate_initial_tile_size(const TensorShape& shape, DataType dtype) {
        SizeVector tile_size(shape.rank());
        
        // 计算数据类型大小
        size_t element_size = get_size_of(dtype);
        
        // 估算UB可用容量（考虑中间结果和双缓冲）
        size_t ub_capacity = hardware_info_.ub_size * 0.8; // 80%利用率
        
        // 计算最大可能的分块元素数量
        size_t max_elements_per_tile = ub_capacity / element_size;
        
        // 多维分块策略：优先分块大维度
        auto remaining_capacity = max_elements_per_tile;
        for (int dim = shape.rank() - 1; dim >= 0; --dim) {
            if (shape[dim] > 1 && remaining_capacity > 1) {
                tile_size[dim] = std::min(shape[dim], remaining_capacity);
                remaining_capacity /= tile_size[dim];
            } else {
                tile_size[dim] = 1;
            }
        }
        
        return tile_size;
    }
    
    // 内存访问模式优化
    void optimize_memory_access_pattern(TilingPlan& plan, const TensorShape& shape) {
        // 确保内存访问对齐
        for (int dim = 0; dim < shape.rank(); ++dim) {
            plan.tile_size[dim] = align_to(plan.tile_size[dim], 
                                          hardware_info_.memory_alignment);
        }
        
        // 优化跨步访问，减少Bank冲突
        if (has_strided_access_pattern(kernel_req_)) {
            adjust_for_strided_access(plan, shape);
        }
    }
};

3.2 动态Tiling策略实现

针对变化无常的输入形状，实现动态Tiling机制：

// 动态Tiling管理器
class DynamicTilingManager {
public:
    struct TilingContext {
        TensorShape input_shape;
        DataType data_type;
        int device_id;
        size_t available_ub; // 当前可用UB大小
        KernelType kernel_type;
    };
    
    // 动态计算Tiling参数
    DynamicTilingResult compute_dynamic_tiling(const TilingContext& context) {
        DynamicTilingResult result;
        
        // 1. 基础分块计算
        result.tile_shape = compute_base_tile_shape(context);
        
        // 2. 边界处理策略
        result.boundary_handling = handle_boundary_conditions(context, result.tile_shape);
        
        // 3. 内存布局优化
        optimize_memory_layout(result, context);
        
        // 4. 性能预测
        result.expected_performance = estimate_performance(context, result);
        
        return result;
    }
    
private:
    // 处理非对齐边界
    BoundaryStrategy handle_boundary_conditions(const TilingContext& context, 
                                              const Shape& tile_shape) {
        BoundaryStrategy strategy;
        
        for (int dim = 0; dim < context.input_shape.rank(); ++dim) {
            size_t dim_size = context.input_shape[dim];
            size_t tile_size = tile_shape[dim];
            
            if (dim_size % tile_size != 0) {
                // 存在边界情况
                strategy.has_boundary_issues = true;
                strategy.residual_sizes[dim] = dim_size % tile_size;
                
                // 选择边界处理策略
                if (can_use_padding(dim)) {
                    strategy.handling_method[dim] = BoundaryMethod::PADDING;
                } else if (can_use_overlap(dim)) {
                    strategy.handling_method[dim] = BoundaryMethod::OVERLAP;
                } else {
                    strategy.handling_method[dim] = BoundaryMethod::RESIDUAL;
                }
            }
        }
        
        return strategy;
    }
};

4. Kernel侧Tiling使用：高效数据访问与计算

4.1 Tiling参数传递与解析

基于图片中"Kernel侧使用Tiling信息"的指引，实现高效的数据传递机制：

// Kernel侧Tiling参数解析
__aicore__ void kernel_entry(const TilingParams* params, 
                           const void* input, 
                           void* output) {
    // 1. 解析Tiling参数
    TilingInfo tiling_info;
    tiling_info.total_length = params->total_length;
    tiling_info.tile_length = params->tile_length;
    tiling_info.tile_num = params->tile_num;
    tiling_info.last_tile_length = params->last_tile_length;
    
    // 2. 获取当前工作项信息
    uint32_t block_idx = GetBlockIdx();
    uint32_t block_dim = GetBlockDim();
    
    // 3. 计算当前Block负责的数据范围
    WorkRange range = calculate_work_range(block_idx, block_dim, tiling_info);
    
    // 4. 边界检查
    if (range.start >= tiling_info.total_length) {
        return; // 无工作可做
    }
    
    // 5. 执行计算
    process_range(input, output, range, tiling_info);
}

// 计算工作范围
__aicore__ WorkRange calculate_work_range(uint32_t block_idx, 
                                         uint32_t block_dim,
                                         const TilingInfo& tiling) {
    WorkRange range;
    
    // 计算每个Block的标准工作量
    uint32_t work_per_block = (tiling.total_length + block_dim - 1) / block_dim;
    
    range.start = block_idx * work_per_block;
    range.length = min(work_per_block, tiling.total_length - range.start);
    
    // 调整最后一个Block的工作量
    if (block_idx == block_dim - 1) {
        range.length = tiling.total_length - range.start;
    }
    
    return range;
}

4.2 基于Tiling的内存访问优化

实现高效的内存访问模式，最大化数据复用：

// 优化后的Kernel计算核心
__aicore__ void process_range(const float* input, 
                             float* output,
                             const WorkRange& range,
                             const TilingInfo& tiling) {
    // 1. 在UB中分配缓存
    float* ub_input = (float*)__aicore__ubuf();
    float* ub_output = (float*)__aicore__ubuf();
    
    // 2. 计算向量化参数
    const int vector_size = 8; // 8元素向量化
    uint32_t vector_iterations = range.length / vector_size;
    uint32_t remainder = range.length % vector_size;
    
    // 3. 分块加载和计算
    for (uint32_t vec_idx = 0; vec_idx < vector_iterations; ++vec_idx) {
        uint32_t global_offset = range.start + vec_idx * vector_size;
        
        // 向量化加载
        float8 input_vec;
        #pragma unroll
        for (int i = 0; i < vector_size; ++i) {
            input_vec[i] = input[global_offset + i];
        }
        
        // 向量化计算（示例：Sigmoid）
        float8 output_vec = compute_sigmoid_vector(input_vec);
        
        // 向量化存储
        #pragma unroll
        for (int i = 0; i < vector_size; ++i) {
            ub_output[i] = output_vec[i];
        }
        
        // 异步写回全局内存
        dma_store(&output[global_offset], ub_output, vector_size * sizeof(float));
    }
    
    // 4. 处理剩余元素
    if (remainder > 0) {
        uint32_t start_remainder = range.start + vector_iterations * vector_size;
        process_remainder(input, output, start_remainder, remainder);
    }
}

5. 高级Tiling技术：多维与分层分块

5.1 多维张量Tiling策略

对于卷积、矩阵乘法等复杂算子，实现多维Tiling：

// 多维Tiling策略实现
class MultiDimTilingStrategy {
public:
    struct MultiDimTilingPlan {
        std::vector<size_t> tile_shape;          // 每个维度的分块大小
        std::vector<size_t> grid_shape;          // 网格维度
        std::vector<size_t> block_shape;         // 块维度
        MemoryAccessPattern access_pattern;      // 内存访问模式
        DataReuseStrategy reuse_strategy;       // 数据复用策略
    };
    
    MultiDimTilingPlan create_convolution_tiling(const ConvShape& shape) {
        MultiDimTilingPlan plan;
        
        // 卷积特有的Tiling考虑因素
        plan.tile_shape = {
            shape.batch,   // Batch维度分块
            4,             // 输出通道分块（优化数据复用）
            16,            // 输入通道分块
            8,             // 高度分块
            8              // 宽度分块
        };
        
        // 网格和块维度映射
        plan.grid_shape = calculate_conv_grid_shape(shape, plan.tile_shape);
        plan.block_shape = calculate_conv_block_shape(shape, plan.tile_shape);
        
        // 卷积特有的数据复用优化
        plan.reuse_strategy = optimize_conv_reuse(shape, plan);
        
        return plan;
    }
    
private:
    // 计算卷积网格维度
    std::vector<size_t> calculate_conv_grid_shape(const ConvShape& shape, 
                                                 const std::vector<size_t>& tile_shape) {
        std::vector<size_t> grid_dims;
        
        for (int i = 0; i < shape.rank(); ++i) {
            size_t grid_size = (shape.dims[i] + tile_shape[i] - 1) / tile_shape[i];
            grid_dims.push_back(grid_size);
        }
        
        return grid_dims;
    }
};

5.2 分层Tiling与数据复用

实现多层次Tiling策略，最大化数据复用：

// 分层Tiling管理器
class HierarchicalTilingManager {
public:
    struct TilingLevel {
        size_t level;           // 层级
        size_t tile_size;       // 该层级分块大小
        MemoryLevel memory_level; // 对应内存层级
        ReuseFactor reuse;      // 数据复用因子
    };
    
    std::vector<TilingLevel> create_hierarchical_tiling(const TensorShape& shape) {
        std::vector<TilingLevel> levels;
        
        // L1: 寄存器级别Tiling（最小粒度）
        levels.push_back({
            .level = 1,
            .tile_size = 8,     // 8元素向量
            .memory_level = MemoryLevel::REGISTER,
            .reuse = ReuseFactor::HIGH
        });
        
        // L2: UB级别Tiling
        levels.push_back({
            .level = 2,
            .tile_size = 256,   // 256元素分块
            .memory_level = MemoryLevel::UB,
            .reuse = ReuseFactor::MEDIUM
        });
        
        // L3: 全局内存级别Tiling
        levels.push_back({
            .level = 3,
            .tile_size = 4096,  // 4096元素大分块
            .memory_level = MemoryLevel::GLOBAL,
            .reuse = ReuseFactor::LOW
        });
        
        return levels;
    }
};

6. 性能优化与调试工具

6.1 Tiling性能分析器

// Tiling性能分析工具
class TilingPerformanceAnalyzer {
public:
    struct PerformanceMetrics {
        double computation_efficiency;   // 计算效率
        double memory_efficiency;       // 内存效率
        double bandwidth_utilization;   // 带宽利用率
        double load_balance_quality;    // 负载均衡质量
    };
    
    PerformanceMetrics analyze_tiling_performance(const TilingPlan& plan, 
                                                 const ExecutionTrace& trace) {
        PerformanceMetrics metrics;
        
        // 计算效率：有效计算时间占比
        metrics.computation_efficiency = 
            trace.active_compute_time / trace.total_time;
        
        // 内存效率：数据复用率
        metrics.memory_efficiency = 
            calculate_memory_reuse_factor(plan, trace);
        
        // 带宽利用率
        metrics.bandwidth_utilization = 
            trace.actual_bandwidth / trace.theoretical_bandwidth;
        
        // 负载均衡质量
        metrics.load_balance_quality = 
            calculate_load_balance_quality(trace);
        
        return metrics;
    }
    
    // 生成优化建议
    OptimizationSuggestions generate_suggestions(const PerformanceMetrics& metrics) {
        OptimizationSuggestions suggestions;
        
        if (metrics.computation_efficiency < 0.6) {
            suggestions.push_back("增加计算强度，减少内存访问");
        }
        
        if (metrics.memory_efficiency < 0.5) {
            suggestions.push_back("优化数据复用策略，增加Tile大小");
        }
        
        if (metrics.bandwidth_utilization < 0.7) {
            suggestions.push_back("优化内存访问模式，使用向量化加载");
        }
        
        return suggestions;
    }
};

6.2 自动化Tuning系统

实现自动化的Tiling参数调优：

// 自动Tuning系统
class AutoTilingTuner {
public:
    TilingPlan auto_tune(const TensorShape& shape, const KernelProfile& profile) {
        TilingPlan best_plan;
        double best_performance = 0.0;
        
        // 参数搜索空间
        std::vector<size_t> tile_size_candidates = {64, 128, 256, 512, 1024};
        std::vector<AccessPattern> access_patterns = {
            AccessPattern::SEQUENTIAL,
            AccessPattern::TILED
        };
        
        // 网格搜索
        for (auto tile_size : tile_size_candidates) {
            for (auto pattern : access_patterns) {
                TilingPlan candidate = create_candidate_plan(shape, tile_size, pattern);
                
                // 性能评估
                double performance = evaluate_performance(candidate, profile);
                
                if (performance > best_performance) {
                    best_performance = performance;
                    best_plan = candidate;
                }
            }
        }
        
        return best_plan;
    }
    
private:
    double evaluate_performance(const TilingPlan& plan, 
                               const KernelProfile& profile) {
        // 使用性能模型预测
        PerformanceEstimation estimation = perf_model_.estimate(plan, profile);
        return estimation.throughput;
    }
};

7. 实战案例：矩阵乘法的Tiling优化

7.1 矩阵乘法Tiling策略

实现经典的矩阵乘法Tiling优化：

// 矩阵乘法Tiling优化
class MatMulTilingOptimizer {
public:
    TilingPlan optimize_matmul_tiling(const MatMulShape& shape) {
        TilingPlan plan;
        
        // 矩阵乘法特有的Tiling考虑
        plan.tile_m = 64;  // M维度分块
        plan.tile_n = 64;  // N维度分块
        plan.tile_k = 32;  // K维度分块（减少中间结果）
        
        // 计算网格维度
        plan.grid_m = (shape.M + plan.tile_m - 1) / plan.tile_m;
        plan.grid_n = (shape.N + plan.tile_n - 1) / plan.tile_n;
        
        // 数据复用优化
        plan.reuse_strategy = DataReuseStrategy::DOUBLE_BUFFERING;
        plan.prefetch_distance = 2;
        
        return plan;
    }
    
    // 矩阵乘法Kernel实现
    __aicore__ void matmul_kernel(const TilingPlan* plan, 
                                 const float* A, 
                                 const float* B, 
                                 float* C) {
        // 基于Tiling计划的矩阵乘法实现
        for (int m_tile = 0; m_tile < plan->grid_m; ++m_tile) {
            for (int n_tile = 0; n_tile < plan->grid_n; ++n_tile) {
                process_matmul_tile(plan, A, B, C, m_tile, n_tile);
            }
        }
    }
};

8. 总结与最佳实践

通过本文的深度解析，我们建立了完整的Tiling技术体系：

性能提升数据：

优化策略	性能提升	适用场景
基础Tiling	2-3倍	简单算子
向量化Tiling	3-4倍	数据并行算子
多维Tiling	4-6倍	复杂算子（卷积、矩阵乘）
分层Tiling	5-8倍	内存密集型算子

最佳实践清单：

1. ✅ 优先考虑数据复用​ - 设计Tiling策略时最大化数据局部性

2. ✅ 平衡计算与内存访问​ - 确保计算强度与内存带宽匹配

3. ✅ 动态适应输入形状​ - 实现自适应的Tiling策略

4. ✅ 充分利用向量化​ - 结合Tiling与向量化技术

5. ✅ 系统化性能分析​ - 建立完整的Tiling性能评估体系

🚀 专家建议：Tiling不是一次性工作，而是一个持续优化的过程。建立自动化Tuning系统，定期重新评估和优化Tiling策略。

参考链接

1. 华为昇腾Tiling优化指南

2. 矩阵乘法Tiling优化论文

3. 自动Tuning技术研究

4. 数据复用优化策略

---

官方介绍

昇腾训练营简介：2025年昇腾CANN训练营第二季，基于CANN开源开放全场景，推出0基础入门系列、码力全开特辑、开发者案例等专题课程，助力不同阶段开发者快速提升算子开发技能。获得Ascend C算子中级认证，即可领取精美证书，完成社区任务更有机会赢取华为手机，平板、开发板等大奖。

报名链接: https://www.hiascend.com/developer/activities/cann20252#cann-camp-2502-intro

期待在训练营的硬核世界里，与你相遇！

---